Several commenters (n+1, n+2, Trevor, math_geek, EconomistsDoItWithModels, Neil, Mark R., possibly others I’ve overlooked) solved yesterday’s probability puzzle correctly, and you can learn a lot by reading their answers. Here’s my version of their argument:
Among those who are prescribed the medicine, there are five kinds of people, represented by the five non-blacked-out squares in the following chart. A, B, C, D and E are the fractions of the population of each type.
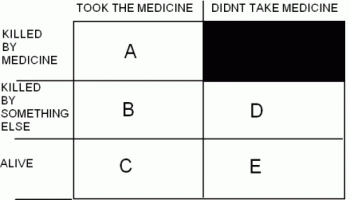
First, we are given that 60% take the medicine, which means 40% don’t take it. That is, A+B+C = 3/5 and D+E = 2/5 . That’s two equations.
Second, we are given that if the man took the medicine, there’s a 90% chance it killed him. If he took the medicine, we know he’s in box A or B. (He’s not in C because he’s dead). So this means that 90% of the people in those two boxes are actually in box A. That is, A/(A+B) = 9/10. That’s a third equation.
Third, it is a natural, reasonable, and simple assumption that death-by-another cause is equally likely among those who take the medicine and those who don’t. That is, B/(A+B+C) = D/(D+E).
That’s a total of only four equations in five unknowns, and it does not determine any of the values A,B,C,D, or E. But rather remarkably, it does determine the ratio A/(A+B+D), which is all we care about. (We know the man is one of the boxes A, B and D because he’s dead, and we want to know what fraction of such people are in box A.)
Indeed, from these four equations it’s easy to get that A=9B and D=2B/3. From this, we have A/(A+B+D)=27/32, which is the answer.
Of course, it’s always possible that the man both had a fatal heart attack and took a fatal dose of medicine. If you unravel the argument above, you’ll see that in that case I’ve counted the man as being in box B, not box A. That’s why I added the clarifying remark that if I say “the medicine killed him”, I mean that the medicine and only the medicine killed him; in other words, “the medicine killed him” means that if he hadn’t taken the medicine, he would have lived. Apparently this remark was unclarifying for many of you, but it does seem to me that it was necessary to add this in order for the problem to be well-specified.
To put this another way, when I ask “What is the probability the medicine killed him?”, the answer depends on whether a heart-attack-plus-fatal-dose-of-meds counts as the medicine killing him. The clarifying remark was meant to remove this ambiguity.
Hat tip to Barry Nalebuff; I’ve adapted this problem from his Problem 2.



I don’t think you second assumption is correct. You are mixing “a priori” reasoning about the population with “a posteriori” reasoning about the specific case.
The equation should be A/(A+B+C) = 9/10
Solving, you get A = 27/50; B = 3/2 D = 3/5 r,
where r = B/(A+B+C) = D/(D+E) is the risk of death from other causes
The probability that a person in the population found dead was killed by the medicine is:
A/(A+B+D) = 1/(1 + 50/27 r)
If r is very small (assuming the population is in good health), then this probability is very near 1.
Your solution 27/32 implies r = 10%
Even better, assuming the risk-from-other causes acts before the medicine has the option of killing the man, we could use A/(A+C) = 9/10, and the probability that a dead person was killed by the medicine becomes: p = (1 – r) / (1 + 50/27 r)
PS: note that as long as the risk due to the medicine A/(A+C) is large wrt the risk from other causes r=B/(A+B+C), the probability that a death is caused by the medicine is near 1, regardless of the other parameters of the problem.
When r is high (assume our man has a mafia hitman after him), then p becomes smaller.
Darn it. I had the right algebra and just messed up the arithmetic :P (At one point I multiplied 0.6*9 and got 0.54 instead of 5.4!)
I read the original source. Your solution is the right one, but your second assumption should read:
“Second, we are given that if a person took the medicine AND IS KILLED, there’s a 90% chance the medicine killed him.” (in other words, the risk associated to the medicine is 9 times the background risk.)
As you expressed it, it would seem as if the medicine had a 90% death risk.
Is there a sensible explanation of how the investigators could have reached their 90% conclusion?
Stefano: I had already specified that the man was dead before saying that if he took the medicine, then there was a 90% chance it killed him.
I stopped putting “clarifying” remarks on my tests. No matter how clear I thought the remarks, invariably they confused the students rather than clarified the question. There must be a law about this.
Nice problem! Mad at myself for not getting it.
I answered my question by looking at the original paper. There were 3 possible drugs that could have killed her. By looking at side effect rates, the investigators estimated that if the person took all three, then the drug in question was most likely to be the killer – 9 times more likey than the other 2 combined.
Very interesting, but it seems like this is a dangerous medicine.
I’ve been pondering the consequence of the assumption that “death-by-another cause is equally likely among those who take the medicine and those who don’t”, and, as a result of this assumption, we must also believe that a person is 10 times more likely to die if they take this medicine than if they don’t.
(Does anyone know if this is an unreasonable number? The probability of dying if you don’t take the medicine is probably small, so 10 times a small number is still small. But would a 10x increase in the probability of dying be acceptable to the FDA?)
Here is why I believe the 10x factor is correct:
First, let’s redefine all of the probabilities in Steve’s chart in terms of the probability of not taking the medicine and dying from other causes:
A = (27/2)*D
B = (3/2)*D
C = 3/5 – 15*D
D = D
E = 2/5 – D
Let’s check against the equations:
A+B+C = 3/5
D+E = 2/5
A/(A+B) = 27/30 = 9/10
B/(A+B+C) = (5/2)*D
D/(D+E) = (5/2)*D
The probability that a person dies given that they take their medicine is:
Pr[dies | take medicine]
= (A+B)/(A+B+C)
= 25*D
The probability that a person dies if they don’t take their medicine is
Pr[dies | don’t take medicine]
= D/(D+E)
= (5/2)*D
The ratio of these probabilities is 10.
In a previous post, I stated that the answer to this question is
(27/50)*Pr[dies|take medicine]/Pr[dies].
Using these numbers, I get
Pr[dies]
= 25*D*(3/5) + (5/2)*D*(2/5)
= 16*D
and
Pr[dies|takes medicine]/Pr[dies] = 25/16,
so the answer is consistent with the one Steve posted: (27/50)*(25/16) = 27/32.
I’m planning to make another post later to point out another consequence of the key third assumption. In short, this assumption could not be applied to a simple model that I used for this problem, but it is not yet obvious why my model and the assumption could not be used together.
No, and that is what makes this a trick question. Many of the comments were fooled by what the 90% was supposed to mean. I am not sure which is the bigger puzzle here — figuring out what Steve is intending the problem to be, or solving the problem.
I don’t see why this information could not be known in principle. The coroners examine a sample of dead medicine-users to determine the cause of death, and they find that 10% died of heart attacks (say)and 90% died from the medicine.
Their first call should be to the FDA to get this stuff off the market right away, but Steve and other libertarians would probably want to let the market decide. :)
Using Steve’s matrix elements and the two stated assumptions, my original answer would have looked like this:
Pr[killed by medicine | dead] = 9/(10 + D/B)
This result only depends on the two stated assumptions. Steve’s additional assumption makes D = 2*B/3, so
Pr[killed by medicine | dead] = 9/(10 + 2/3) = 27/32.
Here is an explanation of why I am a little (only a little) uncomfortable with the assumption. The original information we knew about the problem allows us to specify the elements of Steve’s table as functions of two unknown probabilities:
A = (3/5)*Pm
B = (1/15)*Pm
C = (3/5) – (2/3)*Pm
D = (2/5)*Poc
E = (2/5) – (2/5)*Poc
The two unknown probabilities I’m using are:
Pm = Pr[killed by medicine | took the medicine]
and
Poc = Pr[killed by other causes | didn’t take medicine].
In general, the answer to the puzzle is
Pr[killed by medicine | dead] = 9/(10 + 6*Poc/Pm)
Again, Steve’s assumption sets Pm = 9*Poc. This is clearly a linear approximation to the underlying system, because it is only valid for Poc less than or equal to 1/9. The model I used resulted in the following relationship between Pm and Poc:
Pm = Poc/(Poc + 1/9),
which keeps Pm smaller than 1 for all values of Poc, and is approximately 9*Poc for small values of Poc. With this model, the ratio of Poc to Pm is (Poc + 1/9) so that
Pr[killed by medicine | dead] = 9/(10 + 6*(Poc + 1/9))
which is equal to 27/32 for small values of Poc. If Poc gets close to 1, then the answer gets close to 0.54.
One final comment regarding the challenge to defend an answer of 0.54. What about a model for which Pm = (9/10)*Poc? That is, if the probability of being killed by the medicine given that you take the medicine is equal to (9/10) times the probability that you are killed by other causes given that you don’t take the medicine, then
Pr[killed by medicine | dead] = 9/(10 + 6*10/9) = 0.54.
This would correspond to the medicine making it less likely for you to die. By specifying some relationship between Poc and Pm, we should be able to get any answer between 0 and 0.9.
Thanks for another fun problem Steve.
@Thomas Bayes: This sort of situation — not these numbers — is not uncommon with drugs. Usually it is not the chance of dying tout court but the chance of dying “of condition X” which is high as as a percentage. But as you note that can still be a small risk, except for those with a high risk of X to start with. A tenfold increased chance of dying by spontaneous combustion sounds scary but is safe for most of us, the initial risk being so low, and an acceptable risk is the drug does good. However for some naturally at risk of bursting into flame — Paul Krugman, Keith Olbermann, Anne Coulter — the risk might be unacceptable.
“However for some naturally at risk of bursting into flame — Paul Krugman, Keith Olbermann, Anne Coulter — the risk might be unacceptable.”
That is funny.
Neat. I humbly admit that I thought the answer was 54%, due to my simplifying assumption to neglect the “death by something else” possiblity.
But that is not Steve’s hypothesis in this problem. You have to read his solution to understand exactly what he meant by the 90%.
It is noted in the article that the painkiller in question has since been withdrawn by the FDA.
The increase in very small risk is often used by the media in scare stories of the sort: “The pill doubles your risk of eyeball cancer!”. Since your risk of eyeball cancer is very small, then doubling the risk is probably well worth it for most people, but each such story is followed by lots of people giving up the pill, or whatever it is.
Roger Schlafly:
But that is not Steve’s hypothesis in this problem.
Yes it is.
This is a fascinating puzzle. I now understand that the key to getting an answer without unknown variables is in setting up a particular relationship between the probabilities. It really is a neat trick.
If the goal wasn’t to produce a number for the answer, though, I
would not say that “death-by-another cause is equally likely among those who take the medicine and those who don’t.” Instead, I would say that “death-by-another cause is equally likely among those who take a non-lethal dose of medicine and those who don’t take the medicine,” and I would write this relationship like this:
Pr[death by other cause | took medicine, non-lethal]
=
Pr[death by other cause | didn’t take medicine]
With the non-lethal clause, instead of requiring that D/B = 2/3, we would require that D/B = (2/3)/(1-15*B). The probability that the medicine killed him would then be:
Pr[killed by medicine | dead]
= 9/(10 + D/B)
= 9/(10 + (2/3)/(1 – 15*B))
As I mentioned earlier, B is equal to the probability that the medicine is lethal divided by 15, so
Pr[killed by medicine | dead]
= 9/(10 + (2/3)/Pr[medicine is not lethal])
Of course this approach presents us with an unknown probability, but, if we knew this probability, then this would be a more faithful expression. Suppose, for instance, that we knew that the pharmacy had a bad batch of medicine, and the probability of a particular prescription being lethal was 1/4. Setting D/B = 2/3 seems flawed because 1/4 of the people who take the medicine will probably not have a chance to die from other causes. It seems better to set D/B = (2/3)/(3/4) = 8/9.
Still, I think it is a cool trick. Although I’m not sure it is much more elegant than using the expression I showed above and assuming that the probability of the medicine being lethal is very small. In the end, both approaches seem to rely on this assumption.
The man in the problem is not at all representative of Neil’s condition. I think that you just made the problem impossible again.
Roger Schlafly,
The whole point of the question is that the man is not known to have taken the medicine, just a 60% chance he took it. But if we do know he took the medicine, we’d know that there is a 90% chance he died from it (as opposed to dying from something else). You claim there is no way the 90% estimate could be known, so the question is pointless. I claim it is reasonable to assume there is a way to establish that dead known-medicine-takers died from one cause rather than another, so the question is fine.
Steve,
I believe that any answer in the range 27/50 to 27/32 is consistent with the original question, and I have a slight objection to your answer of 27/32 because I believe it is unlikely that the information available to — or assumed by — the investigators would support this answer.
(Earlier I said that any answer between 0 and 0.9 was possible, but I overlooked the constraints that the investigators’ findings impose on the relationship between the probability of the medicine being lethal and the probability of dying from some other cause. I have corrected that here.)
To defend the answer of 27/50, we’d need to assume that the medicine had a 90% chance of being lethal, that the man was going to die of another cause if he didn’t take the medicine, and that a lethal dose of medicine would kill him instantly. I can envision a set of circumstances for which this would be true.
To defend the answer of 27/32, we’d need to assume that if the man was going to die of another cause, then a lethal dose of medicine would never kill him before the other cause. I can’t think of a set of circumstances for which this would be true. That is, once the man took a lethal dose of medicine, the other cause would always kill him before the medicine could do so.
I’ll outline my reasoning in a subsequent post, and look forward to your response.
Steve,
I now understand why you added the extra clarity. Thanks for the puzzle. I’ve found much to learn.
Saying that
‘the phrase “the medicine killed him” should be interpreted to mean that if he hadn’t taken the medicine, he wouldn’t have died.’
is exactly what you needed to say to constrain the answer to the one you gave.
You might be interested in this plot of the upper and lower bounds for all answers that are consistent with the problem statement (without the extra constraint):
http://dl.dropbox.com/u/1633558/Landsburg/medicine.gif
Your clarifying statement set to zero the probability that a lethal medicine would kill someone who was otherwise going to die of something else, which is the only situation for which the upper and lower bounds are equal to the same number, and the only place that the upper bound can be attained. The lower bound can always be attained.
I still think the only justification for using the clarifying constraint is to get a single answer to the question, not because it is a reasonable thing to do. If the medicine killed him in his sleep one hour before he would have died of a heart attack, then he would have died if he hadn’t taken the medicine, but I think we should still say that the medicine killed him.
I still don’t get it. If there’s a 40% chance he didn’t take the medicine, how could the chance that he died from it exceed 60%? Is the assumption about how (un)likely he was to die anyway the part I’m missing? I read the original problem from the Yale guy. That one is more clear, but I still think this is more about slick word usage than anything else. According to the problem, 40% did not take the medicine. So there must be at least a 40% chance that the medicine didn’t kill him.
Matt: Of those who are prescribed the medicine, only 60% take it. If this man were randomly chosen from the population of those who were prescribed the medicine, then the chance that it killed him could not exceed 60%.
But he is not randomly chosen from those who were prescribed the medicine. He was instead randomly chosen from those who were prescribed the medicine and are dead. Recognizing this is the whole key to the problem.
Here’s the funny thing. Your question, as “clarified”, actually contains no unknowns (in the sense of an internal probability that cannot be calculated), no variables (except population size, which is irrelevant to the task at hand), and instead has pre-ordained all of the values A, B, C, D and E. Had you asked a question that contained unknowns where they might fairly have been expected, it could not have been solved. Plus the “medicine” is actually a poison.
Here’s why:
(1) By stipulating that “the medicine killed him” should be interpreted to mean that “if he hadn’t taken the medicine, he wouldn’t have died”, you have constrained the only possible scenario to one in which:
(a) 90% of those who took the medicine and died can only have died because of the medicine and not because of any “other cause”; and
(b) The other 10% of those who took the medicine and died can only have died because of some “other cause” and not because of the medicine.
(2) Your stated assumption, namely that “death-by-another cause is equally likely among those who take the medicine and those who don’t” therefore means, from (1)(b) above, that the “other cause” will kill 10% of people who have been prescribed but have not taken the medicine.
(3) Given this, the medicine has no effect, for the purposes of the question, except to kill the 90% who have had it prescribed and have taken it but have not been killed by the “other cause”. In particular, if the medicine were capable of saving the life of even one person, no matter how large the sample, it would follow that the probability of a person being killed by the “other cause” is smaller amongst those who took the medicine than amongst those who did not. For this to be possible, the probability that the “other cause” will kill anyone who has been prescribed the medicine but has not taken it would be less than 10%, thus contradicting (2) above.
(4) Further, there can never be a person who, having had the medicine prescribed and having taken it, hasn’t died. In particular, given (1)(a) and (1)(b) above, out of a sample of 30 people who took the prescribed medicine and died, 27 must have been killed by the medicine and the 3 others must have been killed by the “other cause”. If even one additional person (the 31st) had taken the prescribed medicine and lived, it would mean that the probability of not being killed by the “other cause” was better than 10%, which would, again, contradict (2) above.
(5) Plainly, (2) above would be a very objectionable proposition – were it not for the fact that it flows necessarily from (1)(b) above, which is effectively given by your question as “clarified”. In particular, vis-a-vis their respective susceptibilities to dying from the “other cause”, there is nothing in the question to distinguish those who – having been prescribed the medicine – then take it, from those who – having been prescribed the medicine – do not take it (except of course for the fact – irrelevant in this connection – that one group does and the other does not take the medicine). This, then, is not a “natural, reasonable and simple assumption”, but rather a necessary implication of your question as “clarified”.
(6) Likewise, (3) above would be a very objectionable proposition – were it not for the fact that it flows necessarily from (2) above, which in turn flows necessarily from (1)(b) above, which is effectively given by your question as “clarified”. A “medicine” that kills people who would not have died had they not taken it, and also leaves everyone else who takes it to die as if they had not taken it, is not a medicine, but is – in every sense of the word – a poison (although some medicines can be poisonous, only poisons are poisonous without being medicinal – which is what we actually have here).
(7) Moreover, (4) above means, among other things, that C in your published answer is always zero. No-one who takes the medicine as prescribed survives.
(8) Similarly, A, B, D and E are known:
B = A/9 (explicitly given by the question)
D = 2B/3 = 2A/27 (implicit by virtue of the “clarification”, or, if you prefer, your “assumption”)
E = 9D = 18A/27 (implicit by virtue of D being known)
(9) So, your question reduces to: A/(A+B+D)
= A/(A+(3A/27)+(2A/27))
= 27/32
(10) For the same reason, ie. because there are actually no unknowns, the probability of someone who has been prescribed the medicine then taking it and dying from it, ie. A/(A+B+C+D+E), is calculable:
= A/(A+(3A/27)+0+(2A/27)+(18A/27)
= 27/50
= 54%
So 54% is the answer, but to a slightly different question (one, incidentally, that could have been fairly asked even without your “clarification” and its implications).
(11) The difference between answers (9) and (10) above is that (10) above states the probability that a dead person, having been prescribed the medicine, had taken it and died because of it, whereas (11) above states the probability that any person who had been prescribed the medicine would have gone on to take it and die because of it.
Since what a real medicine does, even if it kills some people who might not otherwise have died, is to help some other people, a fair question to elicit the probability of a given medicine having killed any part of the population of people to whom it had been prescribed would have allowed for that medicine also to have saved some other part of that population.
In that case, you could not take it that D = 2B/3. Specifically, D would then be unknown because its relationship to B would depend on E’s relationship to C, ie. what proportion of the population lived after have taken the medicine who would not have lived had they not taken the medicine. Your question has constrained C to zero, and fixed D (and therefore E) relative to B, which is in turn constrained to a percentage of A.
Thus, if, contrary to how it was advertised, the question had allowed for the “medicine” to actually behave like a medicine, only the relationships of A to B and of A+B+C to D+E would have been known, your “assumption” would not have been unjustified, and the question would not have been capable of a solution.
In fairness, you could argue that the question is exactly what you defined it to be. That is helpful as far as it goes, but your published solution states: “That’s a total of only four equations in five unknowns, and it does not determine any of the values A,B,C,D, or E. But rather remarkably, it does determine the ratio A/(A+B+D)”. This, I think, gives the game away.
This expands the explanation in my original comment.
It being given that “if the man took the medicine, then there’s a 90% chance it killed him”, your “clarification”, namely that “the medicine killed him” should be interpreted to mean that “if he hadn’t taken the medicine, he wouldn’t have died”, sets up an implication. In those 90% of cases, since the subject would not have died except for the fact that he took the prescribed medicine, the “other cause” (meaning “another cause”, as you use the term) would not have killed him even if he had not taken the medicine. It follows that any scenario in which the subject dies not having taken the prescribed medicine, but of whom it could be said that he would not have died had he taken the prescribed medicine, is ruled out.
Put another way, then, the chance of the subject being killed by the “other cause” is not reduced by his taking the medicine: Q.E.D.
Accepting that there is no reason to suppose that the “other cause” is not more likely to kill the subject who takes the medicine than the subject who doesn’t, the above means that death by another cause is equally likely among those who take the medicine and those who don’t – which is precisely your stated “assumption”. As demonstrated, this is in truth a necessary implication of the question as “clarified”.
It might be tempting to argue that, where the subject was actually killed by the medicine but would have died anyway had he not taken the medicine (the case which I say you have ruled out), the subject would simply not qualify as having been “killed by the medicine” as defined by your “clarification” (even though, as a matter of fact, he was killed by the medicine). But that argument falsifies your stated “assumption”, which is the key to your published solution. Moreover, it leads to the question posed being incapable of a solution, since D then does not equal 2B/3, and we have no way of knowing what the ratio D:B is.
(Note that the penultimate paragraph of my original comment should be corrected to read: Thus, if, contrary to how it was advertised, the question had allowed for the “medicine” to actually behave like a medicine, only the relationships of A to B and of A+B+C to D+E would have been known, your “assumption” would not have been justified, and the question would not have been capable of a solution.)