 Greg Mankiw, with a hat tip to his son Nicholas, asks for a plot of the function xx, where x is a real variable. The answer he points to (provided by Pedagoguery Software) gives this picture/expanation:
Greg Mankiw, with a hat tip to his son Nicholas, asks for a plot of the function xx, where x is a real variable. The answer he points to (provided by Pedagoguery Software) gives this picture/expanation:
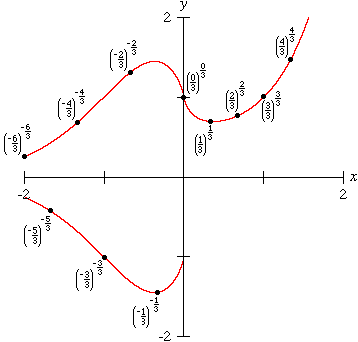
Although the graph does not immediately appear to be a function, closer examination will reveal its true nature…
For negative x, xx is
- undefined if x is irrational,
- undefined if x = odd / even,
- a well-defined positive real number if x = even / odd, and
- a well-defined negative real number if x = odd / odd.
This answer is, of course, correct or incorrect depending on how you define xx. Since the Pedagoguery Software folks (henceforth I’ll call them “the PS folks”) haven’t offered any definition, it’s hard to tell whether their answer is correct or not.
So let’s try to figure out whether any reasonable definition could yield this answer.
The starting point for any reasonable definition is surely to set xx equal to one of the many values of ex Log(x). (This function is many-valued, because, for any value of Log(x), you can always add 2πi and get another one.) It seems clear that the PS folks are interested only in real values (in accordance with the usual elementary school edict that, for example, the square root of -1 is undefined). Given this, it’s a nice little high-school-level exercise to prove that:
| When x is negative, ex Log(x) has at most one real value. Moreover, it has a real value exactly when x can be written as a fraction with an odd denominator, in which case that value corresponds with the value given by the PS folks. |
Aha! So that suggests that the working definition for xx is “the unique real value of ex Log(x) if it exists, undefined otherwise”.
Unfortunately, this doesn’t work when x is positive. For example, (1/2)(1/2) has two real values (the positive and negative square roots of 1/2). There’s also a problem when x=0, where Log(x) is undefined.
So the working definition seems to be “the unique positive real value of ex Log(x) if it exists; otherwise the unique negative real value of ex Log(x) if it exists; otherwise undefined unless x=0, and in that case 1″. This is a perfectly legitimate definition according to the Humpty Dumpty criterion (“When I use a word, it means just what I choose it to mean”), but it’s starting to look pretty ad hoc — sufficiently so that I don’t think anyone could reasonably have guessed it.
So I don’t like this problem!
(Incidentally, if you don’t like multiple-valued functions, the really right way to handle all this is to define the function Log(x) not on the complex numbers but on an appropriate Riemann surface, though even then you need to do a little extra finagling to ensure that 00 comes out to be 1.)



A reasonable value for 00 is 1, as the graph shows.
When I saw the original post by Mankiw, the engineer in me wrote x as:
x = e^(log|x|) e^{j*[1 – u(x)]*pi} e^{j*2*pi*k},
where u(x) is 1 for x>=0 and 0 for x<0, and where k is any integer. Then I wrote x^x as
x^x = e^(x*log|x|) e^{j*[1 – u(x)]*x*pi} e^{j*2*pi*x*k},
which has all the 'problems' you mention, except the same engineer in me is comfortable calling 0*log0 = 0.
When you say you don’t like the problem, it looks like you should say that you don’t like the particular solution provided. I think that the problem is great! It’s easy enough to wrap your mind around, but leads to unexpected places. Your revealed preference (spending time thinking about the problem, graphing it, etc) indicate that you like the problem too.
Mankiw’s marking seems a bit harsh! B- corresponds to what, the top 25%? Surely not more than 15% of grade 11 students are fluent in complex analysis.
Darf Ferarra: Fair enough!
Thomas Bayes:
the same engineer in me is comfortable calling 0*log0 = 0
The mathematician in me is not entirely uncomfortable with this, especially since it gives 0^0 = 1. Sacrificing this would be as unsettling to me a sacrificing 2^2 = 4.
Well done. That made a mind-bendingly simple problem reassuringly opaque.
For those looking for a good book on complex numbers, analysis, and issues with log functions a great book is Visual Complex Analysis by Needham.
It is however a math textbook for a second or third year course; it is well beyond the ‘bright high school student’ level.
Ken B: I love Needham’s book.
@Steve:
I think an idea for a post would be to discuss some outstanding math books accessible to non pure math types, with a description of who might like them: bright high schoolers, or people who took just intor calc, etc. I have recommended a number here over the past couple years.
here of the top of my head are a few
Maxfield http://www.amazon.com/Abstract-Algebra-Solution-Radicals-Mathematics/dp/0486477231/ref=sr_1_1?ie=UTF8&qid=1333637850&sr=8-1 Abels’ theorem for bright high schoolers (!!!)
Nagel, Newmann Godel’s Proof
mathematics http://www.amazon.com/Mathematics-Content-Methods-Meaning-Dover/dp/0486409163/ref=sr_1_5?ie=UTF8&qid=1333637974&sr=8-5 An old but astonishing book: top Russian mathematicians from the 50s with accessible essays on the whole subject. 1100 pages of prose.
Thumbs down for Maxfield’s book. I commented on this way back on a similar thread, but I think the authors spend way too much time on really simple stuff and then blow through the difficult material at the end of the book.
I thought Charles Pinter’s book was 5x better.
I think an idea for a post would be to discuss some outstanding math books accessible to non pure math types
How non-pure you talking? Layman? Professionals in analytic fields? Engineers? Computer scientists?
And what type of math you talking?
I’d be surprised if the average layman could get much more advance than a book like A History of Pi. Here’s a list of similar type books.
Analytic professionals may be able to get into things like number theory.
But to really get to the heart of the matter of even what might be considered “easy” gets hard very quickly. To see the elegance of number theory (probably the most accessible advanced math topic because it deals with the natural numbers, something nearly everyone is familiar with) things can get very hard and very abstract pretty quickly. For example, Fermat’s last theorem is pretty easy for anyone to understand who understands what an integer exponent is.
The proof is not. I’d be willing to bet that no more than 100 people in the world understand the proof. Getting more abstract (going to the general theory of groups and rings) you can get more accomplished and understand more number theory. However, it’s perfectly fine to stick to the concrete examples of the natural numbers and get pretty far in get to some very interesting (and useful) results. Cryptography and coding theory depend on number theory and much of it doesn’t require advance math knowledge.
Advanced analysis (like real analysis and complex analysis), topology, and abstract algebra aren’t really like that. To understand that x^x = e^(x * Log(x)) takes a bit of understanding of pure math.
A better question to ask would probably be “What are some good introductory/interesting books for topic X for non-professional mathematicians?” The more specific X is, the easier it is to answer the question.
If you’re just looking for some mathematical diversions and have some fun, Martin Garnder has pretty much dedicated his career to providing examples. He has written several books.
@Ken:
Well that’s why I said, with a description of who it’s for. Note the warning I attached to Needham. A label is defintely needed.
The big Russian book would be good for someone who has had a semester of calc, to get a broad view of mathematics.
Cambridge’s Open University has a good book called Geometry. I’d recommend that to anyone doing a math, engineering, or science undergrad. Or ambitious folks in the visual arts.
Etc.
In the spirit of Ken’s suggestion, if you are interested in Partial Diff Eqs, and who isn’t, then this is a superlative book
http://www.amazon.com/Differential-Equations-Scientists-Engineers-Mathematics/dp/048667620X/ref=sr_1_1?s=books&ie=UTF8&qid=1333647568&sr=1-1
I wish I’d found that book when I studied PDEs.
Ken B,
I think you’d be hard pressed to find someone who doesn’t think about PDE’s at least a couple times a day:-) I’m almost positive this is the book I used for PDE’s and thought it did a pretty good job.
I liked the counter examples books for analysis and topology. These books really helped clarify a lot of topics and give examples of things that seem mystifying at first (like a continuous function that isn’t differentiable anywhere).
For a set of problems to work, I used Berkley Problems in Mathematics. This has a lot if different types of problems covering most of what a typical math major covers as an undergrad.
To study multi-variable calc (as a refresher since I took calc 3 way back in 1993), I bought these two, both of which focus on the the applications of vector calc in electromagnetics. I’ve only skimmed them, but so far they look pretty decent.
I’ve also used a number of Schaum’s books, but mostly for engineering (like Signals and Systems), not math, and found them a very good value.
@Ken: I probably took my last math class before you were born but as it happens I know and have read both Div, Grad and Student’s Maxwell’s. Both are excellent, and Div Grad is a famous classic.
I liked Rojansky’s rather discursive book on EM, cheap from Dover. he’s very clear on definitions and logical structure.
I don’t buy the claim that the answer is arbitrary.
Imagine a somewhat different problem: instead of being asked to graph X^X, you’re being asked to graph X*X, but you don’t know what * means.
In this hypothetical, you still do understand other mathematical operations. So you start by thinking “whatever X*X means, it has to at least be equivalent to “X / (1/X)”. You then begin to graph that and discover that that doesn’t work when X=0. Your final conclusion: “X*X is arbitrary! I think I know what it means some of the time, but then I need to add a special case at X=0 just to get what the questioner wants!”
Well, no it’s not. “X / (1/X)” isn’t the *definition* of X*X. It’s a method of calculating X*X, and a method of calculating a function can have a domain more limited than the function itself.
Another point is that whether something seems arbitrary can depend on how you word it. For instance, I could collapse “the unique positive real value of e ^ (x Log(x)) if it exists; otherwise the unique negative real value of e ^ (x Log(x)) if it exists” into the single phrase “the largest real value of e ^ (x log(x)) if it exists”. Is that half as arbitrary?
Ken Arromdee: Much of your analogy is well taken, but there’s one important difference: In your analogy, X / (1/X) really *isn’t* the definition of X*X, whereas any plausible definition of x^x is going to look a lot like e^(x log(x)).
Ironically, I first read this post on a Blackberry and it showed the original problem as graphing “XX”. I couldn’t understand what the issue was. I hadn’t seen Steve write such nonsense since the debt-burdening-future-generations issue.
Steve, you say “any plausible definition of x^x is going to look a lot like e^(x log(x))”. But I can think of one definition that doesn’t look like that: define the exponentiation of real numbers a^b in terms of exponentiation of rational numbers and Cauchy sequences of rational numbers.
@Keshav: I’m not sure that works well when you toss i into the mix.
Keshav,
The number b=a^(1/n) is defined as any number such that b^n = a.
Thus, (-1/2)^(-1/2) doesn’t really make sense if you don’t use the definition e^(xLog(x)). After all there is no rational or real a such that 1/(a^2) = -1/2.
For for all positive rational x, x^x makes sense and then x^x = e^(xlog(x)) through the basic properties of rational exponentiation (LR Theorem 1.21), the exponential, and the logarithm (LR pages 178-182). Extending to negative numbers, you have to resort to Log (the complex logarithm) and x^x can really only be reasonably defined as e^(xLog(x)).
Lastly, I’m not sure your definition makes sense. 1/2^1/2 is not rational. Just because xn is rational and you can construct an irrational x from rational Cauchy sequence doesn’t mean you can do that same with xn^xn. Even when xn is rational, xn^xn is not guaranteed to be rational (in fact it almost never will be and if any xn is negative, then it’s not even real), so you can’t define x^x, for real x, as the limit of a rational Cauchy sequence.
*LR = Principles of Mathematical Analysis by Walter Rudin
@Steve: What is a definition?
There are mathematical concepts which are related in certain ways, such that if you pick enough of them as given you can describe the others in terms of the ones you picked. But which ones you pick are arbitrary. I could understand * but not understand / , and explain / in terms of *. Or I could understand / but not *, and explain * in terms of /. Neither one is “the definition” as if some were more elementary than others and there is some order in which you must understand them.
@Ken Aromdee:
There’s a natural hierarchy. Start with Peano Axioms, define N, define Z, define R, define C – all unique in a very strong sense. Define a^b on N and extend it.
Wolfram’s Mathematica favors a slightly different solution (or gets a B- for the real-valued plot):
http://www.wolframalpha.com/input/?i=x^x
Check out the plot of f(x) = sin(e^x).
If you saw that curve alone first, would you guess it had a simple equation associated with it?
Btw it’s been a while since I’ve taken complex analysis, but I think (1/2)^(1/2) is defined as the positive solution only. For instance, there are two distinct solutions to x^2=4, but 4^(1/2) is defined as 2 (and not -2). Does that make sense?
In addition, for -x, the function f(x) = x^x yields complex values sometimes, so the curve is actually shooting up into the z-axis (not depicted in your image) and then coming back into the real-number-only xy plane at times. It’s still a function, I think.
KS: It’s still a function, I think. To make it a true function, you’ve got to pick one value for each x. As you point out, there’s an obvious way to do that when x is positive, but there’s not when x is negative.
“Sacrificing 0^0=1 would be as unsettling to me as sacrificing 2^2 = 4”
f(x,y) = x^y, x,y\in R^+ doesn’t have a well defined limit as (x,y) -> (0,0). If you take the limit along paths approaching (0,0), you might get 1 if you choose the path along y=x, but you might get 0 if you chose a different path, or in fact any positive number, or infinity, or no well-defined limit.
Choosing 0^0=1 makes sense when discussing the function f(x)=x^x, but it makes g(x)=0^(x^2) look rather strange.