Wall Street quants are always trying to dream up new financial products that nobody’s figured out how to regulate. Sooner or later, I suppose, one of them will come up with a bank account that pays imaginary interest. You deposit a dollar and a year later you get an interest payment of i. That’s not “i for interest”; it’s the square root of minus one. I have no idea what that means for economics, but thinking about it is a good way to understand Euler‘s (or, the historical record being unclear, perhaps Johann Bernoulli‘s) breathtakingly beautiful formula

(To follow this, you’ll need to know a little bit about complex numbers, say at the level of Steven Strogatz’s recent blog post at the New York Times. Several of Professor Strogatz’s commenters lamented his omission of the Euler formula. This post is my attempt to fill that gap. You can also view this as my first annual pi day post, slightly belated because 3/14 was a Sunday this year.)

So. With imaginary interest, you deposit a dollar on January 1, and by the end of the year, it’s grown to 1+i dollars, represented by the “Dec. 31” point on the following graph. It’s as if you’d started at the point 1 and traveled upward along the red line to your end-of-year destination.

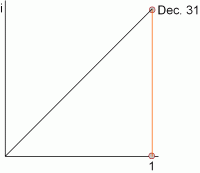
If these accounts prove popular, competing banks will be forced to offer an even better deal— compound imaginary interest. Instead of waiting all year to collect your imaginary dollar, you collect half an imaginary dollar halfway through the year and then continue to earn interest on your new principal of (1+i/2) for the second six months.

You can see this in the next graph. You get your first interest payment on June 30, bringing you from the point 1 to the point (1+i/2) at the upper vertex of the shaded triangle. For the second six months, we have to treat that (1+i/2) the same way we treated your initial principal of 1. That means constructing a triangle similar to the shaded one, but using the blue line as the new base. The upper vertex of that triangle shows us how much you’ve got on December 31.

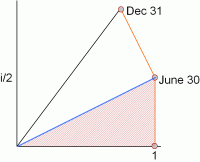
And of course it doesn’t stop there. Before long, another bank offers to compound your interest not twice a year, but four times. How much do you have at the end of the year? Four triangles reveal the answer:

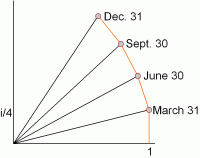
Now take note of this: As you travel along the red lines, from your initial principal of 1 to your new principal balances on March 31, June 30, September 30 and December 31, it looks an awful lot like you’re traveling around a circle. When a new bank offers to compound your interest twelve times a year instead of four, there are going to be twelve much skinnier triangles and the red path around them is going to look even more like a circle.

So when a very competitive bank comes along to offer you imaginary interest compounded continuously, they’ll determine your end-of-year balance by going to the limit and drawing an honest-to-God circle, starting at the point 1, and traveling counter-clockwise a distance 1, like so:

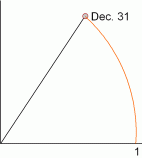
(The December 31 endpoint happens to be at about .54 + .84 i . )

Of course, you might want to leave your money in this account for more than a year. As your interest continues to compound, you move farther around the circle. At the end of two years, you’ve traveled a distance 2, and at the end of three years, you’ve traveled a distance 3, like so:

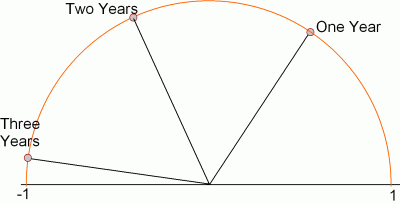
And if you choose to leave your money in the account for, oh, say, about 3.14159 years, then you will travel a distance 3.14159 around the circle, landing at the point -1. (Remember that π, which is just about 3.14159, is the length of the top half of a circle of radius 1.)

Not a bad outcome from the bank’s point of view! You lend them a dollar for a year, and after 3.14159 years, you owe them a dollar! (Of course after another 3.14159 years, you’ll have traveled all the way around the bottom half of the circle and have your original dollar back again.)

Alright, that’s one way to calculate your bank balance after π years. But a faster way is to remember the formula for compound interest: If you deposit a dollar at an interest rate of r for time t, then your ultimate balance is e^{r t}. In this case, the interest rate is the imaginary number i and you’ve invested for time π, so your ultimate balance should be e^iπ.

The bottom line: Our first calculation says your balance is -1. Our second calcuation says your balance is e^iπ. But surely your balance is equal to your balance! Therefore:

Et voila.

Hat tip: The idea of using imaginary interest payments to explain Euler’s formula is inspired by David Mumford‘s article on calculus reform.