 If there is a God, this is the closest you’ll ever come to hearing Him sing. Let me explain.
If there is a God, this is the closest you’ll ever come to hearing Him sing. Let me explain.
The greatest mystery in arithmetic is: How are the prime numbers distributed?
We can start by drawing a “prime staircase” that jumps up at each of the prime numbers, beginning with 2, 3, 5, 7, and 11:
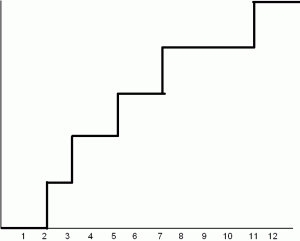
Here’s how that staircase looks when you zoom out far enough to see all the primes up to 100:
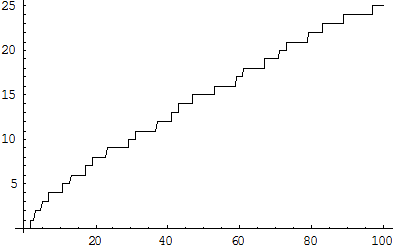
Understanding the distribution of the primes means understanding the shape of this staircase.
For that, we try superimposing a nice smooth curve that tracks the staircase tolerably well:
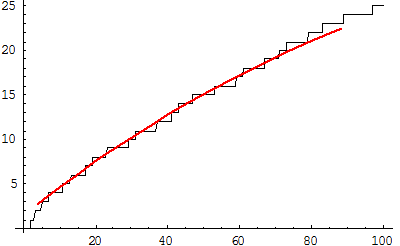
Now the problem is to understand the discrepancies—the difference between the staircase itself and the smooth red curve. Some of those discrepancies are positive (when the staircase is above the curve) and others are negative. If you graph the discrepancies, they look quite chaotic. Here’s what they look like, for example, in the range from 1 million to 2 million:
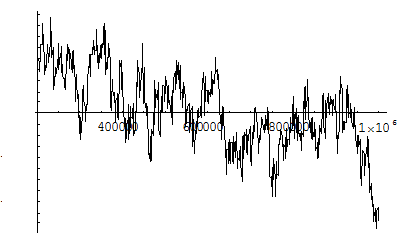
The great 19th century mathematician Bernhard Riemann suggested that we can resolve the chaos by decomposing it into a sum of simple waves.
To see how that could work, here are three nice simple waves:
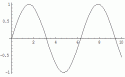 |
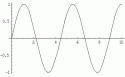 |
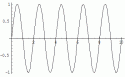 |
If you add these three together, you get something that’s already starting to look a little chaotic:
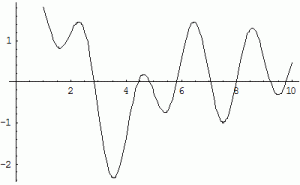
Riemann’s hypothesis was that if you add up infinitely many waves instead of just 3, you should be able to reproduce the extreme chaos of the prime staircase discrepancies. If that’s true, the apparent chaos is not so chaotic after all.
(I should mention that everything I’ve said here is true in spirit but false in technical detail. I am sacrificing accuracy for clarity.)
Now a wave can always be interpreted as a musical note—the distance from peak to peak represents a tone and the height of the peaks represents the volume. So the Riemann hypothesis says in essence that the distribution of primes—the very foundation of arithmetic—is encoded in a piece of music.
We do not know that Riemann’s hypothesis is true—and in fact, proving (or disproving) it is widely considered the single most important unsolved problem in all of mathematics—but we have vast evidence for it, and assuming it is true, we know the first several billion notes.
How do those notes sound? You can listen to them in this MP3 file (the same one I linked to in the first line of this post), which I took from the web page of the mathematician Jeffrey Stopple. (For readers who care about precision, Stopple’s pages are an excellent antidote to the cavalier attitude I’ve taken in this post.) The notes are added one at a time, at intervals of .2 seconds. At the end, all 100 notes play together for 10 seconds. That final 10-second tone represents the sum of the first 100 Riemann waves, which in turn gives a pretty good approximation to the “chaos” of the discrepancies from the prime staircase. This is the music of the primes.



damm that’s funky. its like listening back in time. wasnt the biggest prime number ‘created’ first? =]
How is the red curve derived from the “prime staircase” function? In particular, is it selected using the sum of least squares? Or the sum of least absolute difference?
I never understood why regression analysis selected curves based on the sum of least squares rather than the sum of least absolute values. I understand that the sum of least squares method is computationally desirable, because square numbers are always positive. But I could also achieve the same outcome by selecting functions that minimize the sum of the difference raised to any even-numbered power. What makes squares special?
To be sure, if I picked a curve by minimizing the difference between the data and the curve, raised to the 4th power, I’d place a lot of emphasis on outlier data. But the same is true when I minimize the sum of squares, albeit to a lesser degree.
Minimizing the sum of absolute difference seems to me to be the theoretically purer method for fitting a curve to data.
nobody.really: The red curve is not derived via least squares. It is in fact the graph of the integral of the function 1/log(x), with the constant of integration chosen so the curve passes through zero when x=2. The famous (and quite deep) Prime Number Theorem says that this curve stays pretty close to the staircase, crossing it infinitely many times. (The red curve in the picture is for illustration only; it’s not a terribly accurate depiction of the actual curve.)
nobody.really – The red curve approximation is not a fit based on data, it is the graph of x/ln(x). It’s a miracle mathematically that this curve is the right fit; what do the primes know about (natural) logarithms? Perhaps a better viewpoint is to view the primes as being like elementary particles, with the prime number p having a ‘mass’ of ln(p). Instead of counting the number of primes less than x, one counts the total mass of all primes less than x. In this case the analog of the red curve is just the straight line y=x! This is a theorem, in that it is proven (Prime Number Theorem) that the percentage of error tends to 0 as x tends to infinity.
Thanks! Thought-provoking as ever.
I’m reminded of some of the thoughts for your theology debates, and ideas of freedom and determinism. I sense some people have a lot of emotional investment in the Incompleteness Theorem, quantum mechanics and the Uncertainty Principle – basically, in secular ideas that resist determinism. Somehow these arguments haven’t exerted much of an emotional pull on me.
But this post got me imagining the possibility of a formula to calculate each prime number. Suddenly I’m agitated. Prime numbers are unpredictable and whimsical and free! And moreover, these qualities do not seem to be mere reflections of some human foibles, but reflect something deeply mysterious. To my surprise, I find I have visceral feelings about this.
I guess I’m not as free of religion as I like to imagine….
nobody.really: There is no sense in which either the incompleteness theorem or the uncertainty principle “resists determinism”. Both are purely mathematical phenomena; they don’t tell us anything about the physics of the real world. Quantum mechanics can arguably be interpreted as non-deterministic but it doesn’t have to be, so depending on exactly what you mean, it might or might not “resist determinism”, though perhaps only weakly.
‘a wave can always be interpreted as a musical note—the distance from peak to peak represents a tone and the height of the peaks represents the volume.’
how does this work? i thought that the human ear was only able to discern a narrow band of frequencies in the same way the eye can only see visible light.