Remember the bullet problem from two weeks ago? If not, I’ll give you a few moments to refresh your memory.
Okay. Are we ready?
I am pretty well convinced that 16 bags suffice, as argued by Mike H, Jeffrey, Brian, and Jacopo, and generalized by Categories+Sheaves.
The explanation I liked best was Jeffrey’s. Let me try to illustrate it. (Warning: There’s no way, I think, to make this instantly clear. It will take a little work to understand it. Only you can assess the opportunity cost of your own time!)
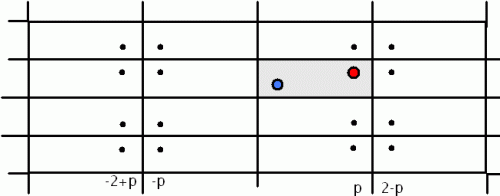
The gray rectangle is the room you’re in.
The blue dot is you. The red dot is the shooter.
With mirrors on all the walls, you’ll perceive yourself as standing in an infinite grid. The graph shows 16 of the grid rectangles, but the pattern continues forever in every direction.
You’re standing at some point (a,b). The shooter is at some point (p,q). You’ll see copies of that shooter at every point with coordinates (2m ± p, 2n ± q) where m and n range over all integers. Sixteen of those infinitely many points are shown in the picture.
Any shot that hits you will appear to come in a direct line from one of these shooters. For example, it might appear to come from the point (4+p, 6-q). The midpoint of that bullet’s trajectory is (2 + a + p⁄2, 3 + b – q⁄2). More generally, the midpoint of any trajectory is at (m + a ± p⁄2, n + b ± q⁄2) for some integers m and n.
Now if m is even, then points with horizontal coordinate m + a ± p⁄2 look exactly like points with horizontal coordinate a ± p⁄2. If m is odd, then points with horizontal coordinate m + a ± p⁄2 look exactly like points with horizontal coordinate 1 + a ± p⁄2. Likewise with vertical coordinates.
To sum up, the midpoint of any trajectory is of the form (m + a ± p⁄2, n + b ± q⁄2), and the location of this point in the original room depends on four things: the parity of m, the parity of n, and the choices for the two ± signs. There are exactly 16 ways to make those four choices, hence exactly 16 possible midpoints for the bullet’s trajectory. Those 16 midpoints are where you want to put your punching bags.
In other words: Draw straight lines from the 16 black dots in the picture (including the black dot that the red shooter is standing on) to your blue self. Mark the midpoints of these 16 lines, reflect them over into the gray rectangle as needed, and that’s where you place your punching bags.
I think it’s also reasonably clear that (for a shooter in general position) there’s no more economical way to block all 16 of these basic trajectories, so that 16 really does solve the problem.
But why are you spending time on recreational puzzles like this one? Yesterday’s puzzle actually matters. Get to work!
Note: The first version of this post contained an error, which Ken B pointed out in comments. This is a corrected version, which I hope I’ve now got right!
Follow up note: The second version contained a more minor error, which AMarchant pointed out. That’s fixed now too.



So I got up through the (2m ± p, 2n ± q) coordinates on my own last Tuesday. But there’s some leap of logic from that to the idea that the bags should be placed at the midpoint. Obviously I didn’t get there on my own, and I thought rikkhill got closest. I suppose if one uses an arbitrary fraction of the line to place all the bags, it becomes clear that the midpoint is the only one that produces the smallest finite number of bags.
Still, I’d love it if someone produced an image of those midpoints reflected in an expanded set of boxes to show that those outside of the closest 16 DO intersect with the other midpoints in some box.
Sean, I think that would be useful too. I also think that a diagram of the corridor version may be clear enough to “see” that the solution is correct, and be a lot simpler.
I think you are reflecting things in the axes not the walls, and this messes stuff up.
In your picture I (blue) am at 0,0 and the red at p,q.
Consider the lower left corner of the gray room rectangle.
It is at -a,-b. 0< a < 1
Consider a line through me (and the left wall of the room) passing through the point with co-ordinates
-2a-p, q
That corresponds to a hit with one reflection off the left wall.
The coordinates of that red image are NOT of the form 2m+-p
Ken B: You are right. One needs to correct for this. I stand by the idea, but the coordinates in the argument all need to be corrected for the fact that the origin of the room is not at the origin of the coordinate system.
More specifically: I should have placed the origin of the room at the origin of the coordinate system in the first place, so that the reflections off the walls and the reflections off the coordinate grid coincide. Now you’re standing at some point (a,b) (presumably not (0,0)) and all of the expressions for the coordinates of points should be adjusted accordingly. Feel free to post the corrected formulas!
@Steve: My initial answer was that you probably couldn’t do it unless there was some nice relation between the a,b,p,q and the room aspect ratio http://www.thebigquestions.com/2012/05/22/tuesday-puzzle/#comment-50952
I don’t think you can just toss +-a into things as you have the other walls etc.
So, I’m still awaiting a proof! :)
Ken B: I’ve edited the post to respond to your objection. Have I managed to get it right this time?
@Steve:
Oh boy, now that you have changed the meaning of p & q there will be confusion referring back to comments and earlier versions!
Anyway I do not (yet) think you have answered my possible counter argument.
I envision reflecting the room along each side. Then refelecting each of those, and so on.
It seems clear you can do this, but I supply no proof.
Now consider a series of reflections moving ever eastward.
The point p,q is first refelcted to p + 2*(L-p) = 2L-p then to 2L + p
then to 4L – p then to 4L + p then to 6L -p then to 6L + p
Relfelcting in the east wall adds either 2p or 2(L-p) depending on parity.
All these point at height q.
Of course I have points at corresponding formulas for q, and then for the reflections of all those etc.
But it seems to me that just in this one row I see a long series of points.
Being lazy I stiop at the construction of 17 trillion of these points in one line and ask if you have blocked then all.
By construction ‘seeing’ is a reflection path so you need to block my sight of each of these points.
And I don’t think your 16 construction does it. Each line has a different slope.
So unless your 16 block mytrajectories somehow (by blocking a reflection) they are not enough.
Ken B: I don’t understand your new objection. You say “unless your 16 block my trajectories somehow….”, but I believe the calculations show that this is in fact the case.
@Steve:
I think you have made assumptions about the room’s dimensions.
room is H high, L long
My construction displays a red point at 2nL – p, q for all odd n
I am at a,b
Midpoint is (2nL-p-a)/2, (q-b)/2
This is not your formula.
You cannot declare L = 1 without me constructing something similar for H. Let H = pi*L for example.
What about reflections of reflections (i.e. inertialess ricochet cycles that do not become closed loops over any x iterations?)?
In that case you need an infinity of punching bags.
@Ken B- Agreed there are an infinite number of space filling(and thus, by definition, lethal)ricochet paths, but is there an upper bound for for non-space filling lethal paths?
vik, the one bag should should still cover all of those cases. Let’s take the case of the shooter choosing to ricochet the shot an even number of times off one pair of walls. (Using North-South directions in the chart above.)
The shooter can shoot directly at you. A bag halfway between you at ( (p-a)/2, (q-b)/2 ) blocks this shot.
The shooter can also bounce the shot twice, off the N-S walls. But these two shot will also be blocked by the same bag at that midpoint. They have to pass through that midpoint as they are just halving the angles of ricochet.
This also means that one bag blocks any shot that bounces an even number of times between the N-S walls. So you’ve blocked half the shots that ricochet only off the N-S walls right there.
The formula Steve gave above just generalizes from this
Very nice. But note that the correct midpoint coordinates are
(m+a/2±p/2, n+b/2±q/2). This doesn’t change the observation that for each of the 16 cases there is a local point (another set of corrections needed) where you can place the bag so that it will appear the the midpoint of all trajectories of that type. It may be helpful to note that the bag may be struck from different directions, depending on m and n.
“By construction ‘seeing’ is a reflection path so you need to block my sight of each of these points.
And I don’t think your 16 construction does it. Each line has a different slope.
So unless your 16 block mytrajectories somehow (by blocking a reflection) they are not enough.”
Ken, what I think you’re perhaps forgetting is that when you extend your lines (trajectories) ever farther down this eastward row of infinite points (and hence decreasing slope), each midpoint you calculate ALSO needs to be reflected infinitely. To take a very simple example, imagine our shooter and target are in opposite corners (this is the special case needing only one bag, by the way). Say we call the coordinates of the red dot (L,W) where L is the length of the room and W is the width, while the blue dot is at (0,0).
The first reflected box to the east of course doesn’t move the red dot as it is on the line of reflection (x=L) so after one reflection the target is still (L,W). and the midpoint is still (L/2. W/2). After the second reflection however, the target is now at (3L, W) and the new trajectory to block has of course decreased in slope. The midpoint of this trajectory however is (3L/2, W/2) which, not coincidently, happens to fall in the center of the first reflected room to the east. But that point is a reflection of the center of the room which is already blocked. Two more reflections gets you a target at (5L, W) and a midpoint of (5L/2, W/2) but that is in the center of the 3rd reflected room which is also a reflection of the center of the original room which is already blocked.
You can see how this pattern will repeat forever. Each further trajectory decreases slope (to arbitrarily small value) but each one passes through the dead center of a reflected room on its way to the target and that center is already blocked.
While this is just a special case, it is illustrative of the overall solution. The difference is that in the generic case each possible trajectory linking the two points has a midpoint that (when reflected back) falls on one of four possible x-coordinates and one of four possible y-coordinates which define the 16 points.
Doing this quickly so might have made a mistake, but I think you’ll find that for a generic room of L by W with points blue: (a,b) and red: (p,q) as above*, the four possible x-coordinates turn out to be 1/2(p-a), L-1/2(p+a), L-1/2(p-a) and 1/2(p+a).
* I’ve taken p>=a for reasons of sign convention and simplicity but as target and shooter are arbitrarily reversible no generality is lost. The same can be done in the y-direction.
You cannot declare L = 1 without me constructing something similar for H. Let H = pi*L for example.
Actually L and H (or W as I called it above) are completely independent with respect to the x and y coordinates of the 16 points. The four possible x-coordinates are determined only by L (and the two points of course) and the four y-coordinates only depend on H (and the two points). You can choose to normalize L to 1 without any loss of generality in H.
Ugh, auto-fill. Posted from different computer and it filled in a different name before I noticed it. Same Brian.
‘vik, the one bag should should still cover all of those cases. Let’s take the case of the shooter choosing to ricochet the shot an even number of times off one pair of walls. (Using North-South directions in the chart above.)’
I think if the puzzle were worded ‘Given an expert shooter (with low I.Q) aiming to kill you in a room as specified, how many bags do you need’- then this line of thinking is helpful.
However in this puzzle the guy is just shooting in a random direction. How can I be absolutely certain (as the puzzle requires)that a ricochet wont hit me from a random direction?
Is there a reason to believe all random shots have non space filling trajectories? If so what is that reason?
A Marchant: Yes, I had minus signs in a couple of places where I should have had plus signs. Thanks for catching this; I’m fixing it now.
@Bryan C: Wghat I was trying to say was this. My formula for the mid point has L in it, Steve’s does not. I assume therefore Steve has normalized L to 1. OK, but then you cannot simultaneous normalize H to 1, so replecae my eat-west construction with a north-south one.
In other words I don’t think Steve’s midpoint formula is right. I’m not forgetting the 16 bags are propagated just like the red point; I am saying the midpoints are not where Steve says they are.
Ken B: You are right that I’ve normalized both L and H to 1. The other commenters are right when they say that doesn’t matter.
Maybe this will help: I’m simply *defining the coordinate system* via the grid I drew. Then I’m working with those coordinates.
@Steve, Bryan, Bryan C, and any other Bryans out there:
An example will clarify the objection I am mkaing.
Consider whose aspect ratio is pi:1, that is a room 1 high by pi wide. I have nornalized the height to one.
The red point is at say (3.1, .8)
Reflection in the east wall, the line x = pi, gives a point at 3.1 + 2*(pi – 3.1) = 2*pi – 3.1
This is not of the form m +- 3.1 integer m.
The formul for the North-south refelctions is of that form, because that’s the direction I normalized.
I am going to save this for my 2 year old son and hopefully in 20 years he can explain it to me.
Ken B:
“This is not of the form m +/- 3.1 …”
That’s because you didn’t normalize the width to 1, which would have made things easier. So instead you got something of the form m Pi +/- 3.1 , and there are still the same limited number of options for the midpoint.
But Steve, there are reflections in the X and Y directions. I am unfolding the room in both directions, filling space. So you cannot normalize both height and width of the room at the same time. What if the room has an irrational aspect ratio? Then either your x or y coordinate formula has a factor L for the aspect ratio.
@Steve:
OK, affine projection.
Never mind.
:)
Just saw the light. Boy do I feel stupid.
Ken B: Despite your “never mind”, let me say this for the possible benefit of others: I DEFINE the width of the room to be one horizontal unit. If the room is 7.6 feet wide, then one horizontal unit is 7.6 feet. Likewise for vertical units. With these units, the room is automatically one unit wide and one unit long. My formulas are calculated with this convention.
@Steve: Yeah, I was gonna suggest you add something.
Here’s another way to see it visually. Use a rubber sheet. If you stretch it uniformly in one direction all lines are stretched, and all questions “are these points on the same line” have the same answer. Alternatley, imagine a grid of wires. Now project the shadow holding the grid at various angles. Once again, ‘colinearity is preserved’ to toss in a little jargon as a distraction to cover up my not seeing this immediately.
Unbelievably low-hanging fruit over at Krugman today.
All you have to do, is compare the two graphs he gives (one for Iceland, one for Estonia) to show they are virtually identical.
He claims the graph he gives for Iceland shows Iceland recoverying nicely because they did what he said they should do (itself a debatable claim) and he claims the graph he gives for Estonia shows how dismally they have done because they didn’t do what he said they should do.
The fruit is so low-hanging that it jumps into your pockets as you walk by!
And the third version contained an even more minor, which was fixed, but introduced an even more minor error….
Ah, the beauty of incremental improvement!
Ken B: One question. You said collinearity is preserved under scaling. However, this is not a conformal mapping: it doesn’t preserve angles if you scale horizontally and vertically by different factors. So doesn’t this affect things, singe reflection angles are involved?
Keshav Srinivasan:
So doesn’t this affect things, singe reflection angles are involved?
Nope. We’re only ever looking at straight lines.
Steve, we are looking at straight lines, but not single straight lines. Rather, we are looking at a zigzag path that consists of a bunch of straight line paths. Now, you may use the mirror argument, and say that the path of he image points in the mirror forms a single straight line going through the infinite grid. But the fact that the image point lies in the same line arises from the angle of incidence being equal to the angle of reflection, and that might not hold anymore because the scaling (by different factors vertically and horizontally) doesn’t preserve angles.
I hope that makes sense.