I’ve just been pointed to this notice of a conference in honor of the topologist Tom Goodwillie‘s 60th birthday.
This reminded me of several things, not all of them related to the relentless march of time.
For example, once a very long time ago (though it sure doesn’t seem that way) Tom asked me a simple physics question that troubled me far more than I now think it ought to have:
A boxcar full of water sits on a frictionless train track. A mouse gnaws a hole through the bottom of the boxcar, in the location indicated here:
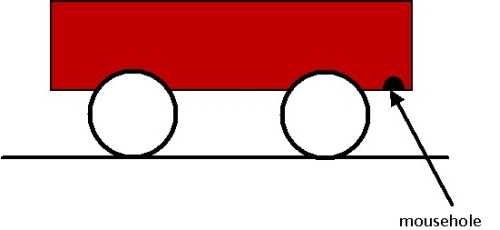
The water, of course, comes gushing out. What happens to the boxcar?



Surely it must depend on the shape of the hole and the fluid dynamics of water? Or should we idealize the hole and the water as well as the boxcar?
The car will go to the left?
If the car would remain at standstill, the water would have effectively moved to the right. Action=reaction so some force somehow should have been exerted on the car?
It moves slightly to the left and stops.
Whilst the water has moved tO the right, it exits the system with no net rightwards momentum, so the boxcar cannot draw any net leftwards momentum.
However the centre of mass of the entire system must remain (left-right) stationary so the boxcar must move slightly left to account for all the water moving right.
The box car doesn’t move.
there is no external force being applied on the box car to make it move.
I would guess that it would move to the left in response to the water moving right. Since the ice is frictionless, the wheels shouldn’t turn.
The water level within the boxcar will slope downwards from left to right.
This causes the pressure within the water to be higher on the left than the the right…
…which accelerates the water from left to right, allowing it to escape through the hole.
But it also means that the pressure exerted by the water on the interior left surface of the boxcar is greater than that on the interior right surface…
…which accelerates the boxcar from right to left.
Since the boxcar is on tracks its motion is constrained to either left or right. The hole (and thus the resultant jet of water emitting therefrom) is perpendicular to the direction the car may move and so no motion occurs.
I think Andy Wood has it mostly right.
The hole is in the side, so the exiting water’s thrust is
perpendicular to the tracks. Initially, nothing happens.
The water leaving makes the right side lower. Water flows right,
implying a force on the left side. This flow is stopped by the
right wall. Result: the force on the right wall balances out the
force on the left wall. No net effect.
Except: some of that flow exits through the hole instead of being
stopped by the right hand wall. Result is that the outgoing stream
isn’t quite perpendicular and there’s a small thrust to the left.
Physics is hard, but I think it stays stationary, and informally, here’s why. We assume the mouse hole is small and the water drains slowly.
Suppose the water draining did impart a horizontal force on the box car causing it to move. You ought to be able to counteract that force by setting the boxcar on an incline plane which counteracts the imposed force and the car would then be stationary (the slope of the incline plane would decrease to zero as the water drained to maintain the equilibrium). However, if the car was on such an incline plane, the water would still be draining downward (the way gravity goes) from the mousehole and no additional horizontal force would be imparted by the water. Now you have a car on an incline filled with water and nothing counteracting it, which means there is no equilibrium, a contradiction.
The effect of the flow missing the right wall is miniscule with a
small hole, but it’s there. That’s why the frictionless track is
important. (I suppose the boxcar has wheels so that it can handle
the condition where the frictionless track ends and the normal track
begins.)
Try this thought experiment. Suppose, instead of a hole, the entire
right-hand third of the boxcar wall suddenly vanished.
To me the only force that impacts the car is vertical, so the car stays in place assuming regular gravity. But then, I am not a physics expert at all. I wonder if part of the riddle is drawing the arrow in such a way that it implies water coming out out the left?
Love these two points:
“Since the ice is frictionless, the wheels shouldn’t turn.”
“(I suppose the boxcar has wheels so that it can handle
the condition where the frictionless track ends and the normal track
begins.)”
But I think the wheels are valuable in that they constrain movement to R^1.
I think DB is correct.
Moves to the left but stops.
Assuming water lows straight down out the hole.
.
I am thinking of a trolley with a tank of water at one end. What happens if I pick up the tank and carry it to the other end of the trolley? I presume the trolley moves in the opposite direction because of the force exerted by my feet. I think it stops though, when I finish carrying it. My stopping exerts a force in the opposite direction just enough to stop the trolley. So in this case the trolly moves a fixed distance to the left.
If I pump the water from one tank to another, I think the same thing will happen. The trolley moves a fixed distance down the track to the left.
The same will happen if I use gravity instead of a pump. However, this is not the same situation as the question, because in the mousehole example the water does not stay on the trolley.
If I let the water flow from one tank to the other, and then let it out the bottom of the second tank onto the track, there will be no further movement. I think that will be the case in the mousehole example.
My apologies for not posting more earlier: I was on a phone and cleaning my teeth when I wrote that. I realise that I did what people who are wrong do: posted an answer without proof / incontrovertible explanation.
Framing:-
This is a one-dimensional (left-right) system without friction. We can ignore all other forces and dimensions: they are of no interest to our box car’s motion.
We don’t really care what happens to the water once it hits the ground. Safest to assume there is no ground and it falls forever. Bad news for the mouse.
Approach:-
With problems like this, you can usually look at forces and pointwise analysis or look at the Hamiltonian and system-wide analysis. In this instance is it considerably easier to look at the system than to consider each water molecule.
Constraint:-
It is a “dividing-body problem” with no external forces. This means that:-
i) the overall system momentum is conserved (ie the centre of mass of the system remains always at rest in the observer’s inertial frame).
ii) the sum of the momentum vectors of the parts divided body are zero in that frame.
Conclusion:-
As water starts to flow out of the hole, the body divides into the “part-full boxcar” (centre of mass in middle of boxcar) and the exited water (centre of mass aligned with hole). The centre of mass of the whole system is then offset towards the hole (from the point of view of the boxcar) — a little at first, and then increasingly as the mass of exited water (and its contribution to the weighted average position increases).
Since i) means that the centre of mass of the whole system may not move in the inertial frame, the boxcar must be offset to the left to leave the centre of mass in the same place.
Notice that this means the water follows a trail leftwards as it exits the boxcar because the hole moves with the boxcar: this problem isn’t as simple as moving all the water to one end of the boxcar and then letting it all flood out (the thought experiment conducted above).
The orientation of the hole means that water falls out, rather than jetting out left or right. It carries no momentum in the inertial frame*. At the end of the process, when the bodies are fully divided into boxcar + exited water the sum of the momentum vectors must remain zero so the boxcar’s momentum must be zero. It is stationary in the intertial frame.
So the boxcar moves to the left to keep the centre of mass stationary and then stops when the water is all exited.
Hard problem: What is the maximum speed of the boxcar? When does it occur?
* What might bother you is that if the boxcar is moving leftwards whilst the water is exiting, does the water not carry leftwards momentum away from the boxcar (so it should be net rightwards at the end). It doesn’t.
The car will remain still. There is not outside force on the car in the horizontal direction. Therefore, no net acceleration can happen. F=MA.
I hit submit too soon.
The center of mass of the car does not move. However, within the car, the center of mass moves. Surprisingly, the center of mass moves to the left relative to the front and back of the car. The means that the car will appear to move to the right.
At some point, the center of gravity will start to move back to the right relative to the front of the car and it will appear to rock back to the left.
In the long run, it will not move since there is no outside force in the horizontal direction.
Interesting, center of mass car + water stays put. Can’t answer the extra credit question without the mass & volume of the car & size of the mousehole I presume?
Now the meta-question: if there are people on the track do I have the right to push someone in front of the moving trolley? (Or shoot the mouse?)
this is my take: the water flows left to right, and the question is how much idealized liquid the water is. Is there any viscosity, friction? If yes, the friction between the (left to right flowing) water and the car should tend to move the car to the right!
“center of mass car + water stays put”
That was my first thought. Water COG moves to the right (initially), so car COG must move to the left. Assuming the water is much heavier than the car, the last of the water ends up falling to left of the original COG.
I wrote earlier that:-
“* What might bother you is that if the boxcar is moving leftwards whilst the water is exiting, does the water not carry leftwards momentum away from the boxcar (so it should be net rightwards at the end). It doesn’t.”
This is a baseless assertion. So according to my previous rule must be wrong. I’ve been driving for an hour and it’s been bothering me all the way home. I despise myself for my lack of rigour.
So the initial action of the boxcar is to the left, however that means the stream of exiting water exits with leftwards momentum, which must cause the boxcar to slow and reverse direction, eventually travelling rightwards when all water is gone.
So:-
Boxcar moves to the left to keep the centre of mass of the system constant and then it slows and moves rightwards as the car drains to balance the leftwards momentum in the exited water (and mouse).
…of course the same argument applies as the car moves back towards the right: it dumps rightwards momentum in the waterflow.
So the question is whether it sets up an oscillating system moving left and right, damping itself, or whether one of the directions dominates and it flies off.
The answer is unclear without actually doing some maths, I think. The principle in action is that the rate of flow is proportional to the height of the water and so more water flows out at the start than at the end. The mass is therefore exponentially decreasing over time whereas the position of the boxcar is based on a weighted average of the CoM. I’m betting that the exponential trumps the linear action every time so I’m back with my second answer: there is no oscillation — the boxcar moves off leftwards, slows, reverses direction and moves rightwards forever.
That’s not a proof, but good enough for me to go and open a beer.
“Tom asked me a simple physics question that troubled me far more than I now think it ought to have”
One sympathises.
Frankly, it’s all beyond me. My math skills stopped somewhere around decimals and fractions, and my puzzle-solving at “If a southbound train leaves the station at 3:00 pm, and …”)
But the commenters who conclude that the boxcar moves also keep saying that it stops at some point (except, I now see, db @ 20). If the track is frictionless, doesn’t the car continue to move, once started?
Imagine the water as hole shaped tubes standing on end in the wagon. They slide out the hole one by one. After the first one how do they got over the hole? By a force applied to move them right. This force must come from the wagon, so the wagon moves left.
Alternately the centre of mass must stay at rest, but the water ends up on the right. Hence the wagon moves left.
Oops I mean the horizontal component of the centre of mass.
If one inflates a balloon, then releases the opening, it flies off in the opposite direction of the opening. I assume the same basic dynamic occurs whether the pressure being relieved involves air or water. But the whole is on the left, and I’m assuming the tracks keep the entire boxcar left-right stationary, precluding movement. And (just intuitively) I don’t think the fact that the whole is nearer one end than the other translates into force moving the boxcar in the direction of the other end.
So I’m left with: No movement left-right or forward-backward.
But there would/could be movement upward (even if undetectable to the naked eye) due to the reduction of downward pressure compressing parts below the contents, and there similarly would/could be inward movement from the walls.
Oh, and if some of the water, after hitting the ground, splashes up and hits the back of a wheel, I assume that would push the boxcar forward (opposite direction from the end near the hole), although I’m not sure whether or not that depends on how high on the wheel the water hits (and is it possible that hitting below some point would turn the wheel such that the boxcar would move backward, and if that would depend on friction between water and wheel).
If I’m interpreting the drawing correctly, the water flows to the right, and the wagon moves to the left. Not sure what seems troubling about that. The really odd thing to me about fluid mechanics is that it doesn’t matter which way the water flows through the “pipe”. Regardless of whether the water is spilling out TO the right, or being pumped in FROM the right, the wagon will be pushed to the left.
db is correct. The center of mass preservation is newton’s second plus Noether’s theorem.
“the boxcar moves off leftwards, slows, reverses direction and moves rightwards forever.”
The boxcar must stop if the center of mass is to be preserved at its initial value.
It depreciates.
(Economics: It’s just not that hard.)
It seems to me, unless the hole has an infinitesimally small diameter, that the water jet will have a small rightward momentum component. I would think the water pressure would be very slightly higher on the left side of the hole than on the right, because the water on the left of the boxcar must flow towards the right to exit through the hole, and the water (initially at rest) will not flow horizontally unless there is a slight horizontal pressure gradient.
If the water jet exiting the hole has a non-zero rightward momentum component, that will generate thrust which causes the boxcar to accelerate to the left. After the last of the water exits the hole, the boxcar will be moving at a constant velocity to the left.
The tracks will keep the boxcar from moving sideways. The water level in the boxcar will slowly fall, but the boxcar will not move.
Kinda funny that some people think they know (objectively) that the hole is on the right (or left) side. Could be either.
@34: “in the location indicated here.”
@30: Nope. The water stops moving right because of friction on the ground, after it has left the wagon. But that won’t affect the wagon.
Here’s a simpler puzzle. Inside the box car there is a partition that runs from the upper left to lower right and the water is in the upper part. As it runs out consider the forces. Gravity pulls the water down, and the partition pushes it at right angles to itself: partly up and partly right. So the water pushes back partly left. But it’s fundamentally the same thing here.
Re: my #34, my bad (ironic, too). I assumed, based on glances at some comments, that when people said the hole was on the right they meant the hole was on the right side of the boxcar (near the front of the boxcar, as opposed to on the left side near the rear of the boxcar). I realize now people meant just right of center of the boxcar as we view it. Sloppy error on my part.