Today is the 165th birthday of Georg Ferdinand Ludwig Philipp Cantor, the mathematician who indirectly inspired me to major in math. In my first few semesters of college, I was at best an indifferent student, finding little inspiration in the humanities majors I was bouncing around among, playing a prodigious amount of pinball, and attaining (according to rumor) history’s first-ever grade of C in Peter Regenstrief‘s Poltical Science 101. Then one day, my friend Bob Hyman happened to mention that some infinities are larger than others, and set my life on track. This—the vision of Georg Cantor—was something I had to know more about. Before long I was immersed in math.
What does it mean for some infinities to be larger than others? Well, for starters, some infinite sets can be listed, while others are too big to list. The natural numbers, for example, are already packaged as a list:
 |
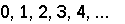The integers, by contrast (that is, the natural numbers plus their negatives) aren’t automatically listed because a list, by definition, has a starting point, whereas the integers stretch infinitely far in both directions. But we can fix that by rearranging them:
 |
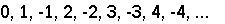So the integers can also be listed.
The positive rational numbers (that is, numbers expressible as fractions) appear even harder to list than the integers, because they have no immediate successors. What is the next rational number after 1/2, for example? Answer: there is no next number. Between any two rationals lie infinitely many more.
We can still list them, though—after a suitable rearrangement of course. There are many ways to do this; here’s probably the simplest: First list all the fractions whose numerator and denominator add to 2, then all the fractions whose numerator and denominator add to 3, then all the fractions whose numerator and denominator add to 4, then 5, and so on, like so:
 |
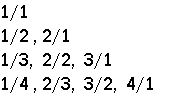and finally string them all together:
 |
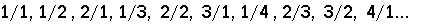There’s some repetition here (for example, 2/2 is the same number as 1/1), but just cross out the repeats and you’ve got your list.
What if you wanted to list all the rational numbers, both positive and negative? Easy! Just combine the two tricks we’ve already used. Start with the list just above, and stick in the negatives:
 |
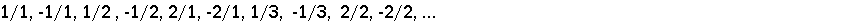Now the only missing rational is zero, which you can throw in anyplace you like—say at the very beginning.
At this point you should begin to suspect that any infinite set can be listed, given enough cleverness. Not so, though. Let’s try to list all the real numbers—that is, all numbers expressible as (possibly infinite) decimals—between 0 and 1.
Now offhand, I can’t think of any way to do this, but that doesn’t prove anything about the real numbers; it might just prove I’m not as clever as I ought to be. But Cantor, with one incredibly simple argument, demonstrated that no attempt to list those real numbers can be successful.
Here’s the argument. Suppose you believe you have managed to list all those real numbers. Maybe your list looks something like this:
 |
(For convenience, I’ve displayed this list vertically instead of horizontally, so the first item on the list is .8410729…., the second is .1415926…, and so on.) Now I’m going to prove you wrong—that is, I’m going to prove your list is incomplete—by writing down a number that’s definitely missing. First I write down a decimal point. Then I write down any first digit other than 8 (say 6). This insures that the number I’m writing down is not the same as .8410729….. Then I write down any second digit other than 4 (say 5). This insures that the number I’m writing down is not the same as .1415926….. Then I’ll write down any third digit other than 3 (say 7). This insures that the the number I’m writing down is not the same as .3333333….. Continuing in this way, I get a number
 |
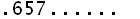that is definitely nowhere on your list.
(If it bothers you to imagine that I could make infinitely many choices, just imagine that I make all the choices at once by applying some fixed rule. For example: Whenever I need a digit other than 1, I’ll pick 7; whenever I need a digit other than 2, I’ll pick 5…)
If you say “oops, I forgot that number; I’ll stick it in my list somewhere”, I’ll just pull the same trick again and find another number that’s not on your list. So no matter how clever you are, you can never list all the real numbers—or even just the real numbers between 0 and 1.
But we saw that there is a way to list all the rational numbers. So in what turns out to be a profound and fundamental sense, the infinity of real numbers is bigger than the infinity of rational numbers.
With that discovery, Cantor taught the world how think about infinity, rocked the foundations of mathematics, and, with a lag of a hundred and some years, changed my life.
I fear you are confusing or conflating ‘size’ and ‘listableness’ (susceptibility to being listed).
What does listing things have to do with their size?
I can list the planets in our solar system, but I can’t list the possible combinations of snowflakes. Still, I’m pretty sure most planets are bigger than most snowflakes.
What does it mean for an infinity to be ‘small’?
Ross Parker:
Two finite sets have the same size if and only if they can be put in one-to-one correspondence with each other. Bertrand Russell illustrated this point by observing that at a large table that has been set for dinner, you can know that the number of forks is equal to the number of knives (that is, the set of forks and the set of knives have the same size) without counting them, as long as there is one fork and one knife at each place setting; this establishes the needed one-to-one correspondence.
Cantor’s idea was to carry this criterion over to infinite sets. To list a set is the same thing as to establish a one-to-one correspondence between that set and the natural numbers. (The first item on the list corresponds to the number 1, the second to the number 2, etc.). By this criterion, sets that can be listed have the same size as the set of natural numbers; sets that can’t be listed are larger.
I seem to remember something about pairing one element in an infinity with another in another infinity. You can pair an integer with a natural number and remove from the list. You can keep doing this for every member of the sets, so they are in some way “the same size”. This is somewhat against intuition, as the integers go backwards as well as forwards, so might be thought of a “larger”. You cannot pair a natural number with each member of the real number set, so the real number set is “larger” than the natural number set. In a sense, there will always be some real numbers “left over”.
I’m still confused about why uncountable and countable sets are “different” sizes. We know that the rationals and the irrationals are dense in the reals. If there are more irrational numbers than rational numbers, then there must be at least one pair of irrational numbers that don’t have a rational number in between them, contradicting the density of the rationals in the reals.
JLA: The definition of “different sizes” is that they can’t be put into one-one correspondence. The rationals and irrationals can’t be put in one-one correspondence; that doesn’t contradict the fact that both are dense in the reals.
JLA: Each rational number can be used many many times as the rational number between a pair of real numbers. If each pair were assigned exclusive use of a rational number in between, then, indeed, there would not be enough to go around.
So, if the number of natural numbers is n, for example, then the number of integers is 2n. The number of rationals is n*n, and the number of reals is infinitely more (n*n*infinity, since there are infinitely many reals between two rationals), and can’t be represented. Is that why we can say that the natural numbers, integers, and rational numbers are countable, while the reals are not?
I got the same shock when I read Infinity and the Mind, by Rudy Rucker.
Too late for a mathematics major, though.
http://www.amazon.com/Infinity-Mind-Philosophy-Infinite-Princeton/dp/0691121273/ref=sr_1_1?ie=UTF8&s=books&qid=1267627120&sr=8-1-spell
Al V.: If the number of natural numbers is n, then the number of integers is 2n. But we’ve shown that there are as many natural numbers as integers, so n=2n. The number of rationals is n*n, and we’ve shown there are as many rational numbers as natural numbers. Therefore n=n*n.
The number of real numbers turns out to be 10^n (because to specify a real number you have to choose one of 10 digits in each of n locations). (It’s also 2^n, because you could write your real numbers in binary notation instead of decimal). But you can’t jump to the conclusion that 10^n is greater than n; that requires proof, and the proof (due to Cantor) is in the blog post.
“Countable” means “the same size as the set of natural numbers” so yes, that’s why we say the naturals, integers and rationals are countable but the reals are not.
Imagine you run the front desk at a hotel with a countably infinite number of rooms. Imagine further that all of the rooms are occupied. A man shows up and asks for a room. Can you give him a room?
Assume that you can shuffle people around by assigning them to new rooms. But you must give everyone a key with a room number on it. You can’t give anyone the “∞” key, because there is no such key. And even if there were such a key, they’d have to walk forever to get to the room, so that doesn’t seem fair.
What if a bus with an infinite number of people in it shows up, and they all want rooms?
What if an infinite number of busses each with an infinite number of people show up, and they all want rooms?
(Sorry about the poor formatting above. Beta version of a web browser.)
Imagine that you run the front desk at a hotel with a countably infinite number of rooms. Imagine further that all of the rooms are occupied. A man shows up in the lobby and asks for a room. Can you give him a room?
Assume that you can shuffle people around by assigning them to new rooms. But you must give everyone a room key with a number on it. You can’t give anyone the “∞” key, because there is no such key. And even if there were such a key, they’d have to walk forever to get to the “∞” room, so that doesn’t seem fair.
What if a bus with an infinite number of people shows up, and they all want rooms?
What if an infinite number of buses each with an infinite number of people show up, and each and every one of them wants a room.
When I was in high school and I learned about the different infinities in math class I was so confused that N+N=N. It just never made sense to me. I still think that when something is twice as big as something else then it is bigger. I still think that when one list contains all the numbers on a second list and contains a number that is not on the second list then the first list is bigger than the second list by at least one. N+1=N.
But then I realized that if you threw a dart at the wall of all real numbers then there is a 0% chance of it hitting a rational number. The real number has no chance of repeating (like 1/3) and no chance of ending in an infinite number of 0’s (like 1/2)
I just don’t remember why the idea of showing that your decimal list doesn’t contain a number because I will pick the number with a different digiit is any different than saying that -2 is not on a list of positive numbers.
Of course, now I spend all day playing with a non-linear optimizer to try and steal money from the government so I really don’t need to remember.
It seems
This is something i have always wondered. If you have a container with an infinite number of blue balls and an infinite number of red balls what is your chance of removing a red ball? What if the blue balls were equal to the number of reals and the red balls equal to the integers? What if the red balls were equal to the number of irrationals? What are your probabilities for picking a red or blue ball in each of these cases?
Neil Wilson:
I just don’t remember why the idea of showing that your decimal list doesn’t contain a number because I will pick the number with a different digiit is any different than saying that -2 is not on a list of positive numbers.
This is the crux of the entire matter. If you attempt to list the integers, and if you do it stupidly (say by listing all the positive integers first) then your list might omit -2. But if you do it intelligently, as in 0,1,-1,2,-2,…, then your list will be complete.
By contrast, if you attempt to list the real numbers, it doesn’t matter how smart your are. Any list you come up with will omit something or other (though of course different lists will omit different things.)
Jerome: Your question is not entirely well posed because you havent told me exactly how you’re going to choose one ball from an infinite collection. But on any reasonable interpretation, if there’s a blue ball for ever real and a red ball for every integer, then the probability of picking a blue ball is one.
One way to convince yourself that this is plausible is this: when you choose a ball, it’s got a number on it. What is the chance that the first digit to the right of the decimal point is zero? Answer: 1/10. What is the chance that the first *two* digits are both zeros? Answer: 1/100. The first three digits? 1/1000. And so on. Now what is the chance that ALL of the digits to the right of the decimal point are zeros? (That’s what it takes to have an integer). It’s got to be smaller than 1/10, smaller than 1/100, smaller than 1/1000, smaller than 1/10,000….. and the only number that’s smaller than ALL of these is zero. So that’s the chance of chossing a red ball.
Here’s an interesting paradox:
You can prove that the infinite set of *subsets* of the natural numbers, is larger than the set of natural numbers. The method is basically the same as the diagonal method used to prove that the set of real numbers is larger than the naturals: You line up the natural numbers in the left-hand column, and the subsets in the right-hand column. Then you can construct a new subset by making it different from the nth subset at the nth counting number — in other words, if the number n IS in the nth subset of your list, then it’s NOT in the new subset you’re creating, and vice versa. Therefore it’s different from every subset of the list.
You can generalize this method to prove that the set of *subsets* of a set, must be larger than that set. So the infinite number of subsets of the real numbers, is larger than the real numbers. Therefore, for any set, you have a set which is larger.
Here’s the paradox: Consider now the set of *everything*. All objects, all atoms that make up those objects, all real numbers — and all *sets* of things, all subsets of those sets, and all subsets of the set of subsets, and so on. Every Thing. If it would make grammatical sense as a noun, then it’s in.
Nothing can be larger than the set of everything because it contains everything. But we just proved that for any set, the set of subsets is larger, right?
I have no idea what the resolution to this paradox is. I know that, technically, the “set of everything” is not considered a “set” — it’s too big, so it’s a “class”, not a set. But I’m not sure how that terminology resolves the paradox. Can it be put in one-to-one correspondence with its subsets, or not? On the one hand, it should be at least as big as its subsets, since it contains all of its own subsets (along with everything else). On the other hand, the diagonal method proves that you can’t put anything in one-to-one correspondence with its own subsets.
Bennett: I’m adding this paradox to my list of things I really ought to blog about.
The bottom line of that blog post will be something like this:
When we set out to axiomatize the natural numbers, we write down some plausible axioms (e.g. the Peano axioms) and hope they will characterize the natural numbers. And we always fail, because there are always structures *other* than the natural numbers that also satisfy our axioms. Nevertheless, out of all those structures (which are called “models of arithmetic”) there is one standard model which is what we know we have in mind.
When we set out to axiomatize set theory, we write down some plausible axioms (e.g. the Zermelo Frankel axioms) and hope they will characterize the universe of sets. And we always fail, because there are always multiple structures that satisfy those axioms. We call those structures “models of set theory”. But here the analogy with arithmetic breaks down, because it’s not at all clear that we can pick out one “standard model” that corresponds to what we really had in mind all along. Instead, it seems likely that our thoughts were fuzzy enough that we never had any particular model in mind to begin with.
So when we talk about “the natural numbers” we have something very particular in mind, even though we can’t characterize it with axioms. By contrast, when we talk about “the universe of sets” we have only a very fuzzy picture in mind and are not really thinking about any one thing in particular.
“The integers, by contrast (that is, the natural numbers plus their negatives) aren’t automatically listed because a list, by definition, has a starting point, whereas the integers stretch infinitely far in both directions.”
i find it interesting that you gave these lists direction as if they were vectors.
theres another reason why numbers dont exist somewhere in this discussion. i can smell it.
Steven
If you are interested you might be able to read Cohen’s book Set Theory and the Continuum Hypothesis, out in Dover. It deals with “forcing” a mehtod Cohen invented to show the CH is independent of ZF. (Godel proved consistency.)
Ken Braithwaite: I did work through a substantial part of Cohen’s book many many years ago. It also helped a lot to have the Lawvere/Tierney reworking of Cohen’s argument close at hand.
Prof. Landsburg,
Maybe I have missed something, but it appears to me that the only difference between attempting to list all of the real numbers and all of the natural numbers is that, with the former – if I am methodical about it – you will still be able to find numbers I have not listed between those I have.
It seems that it is still equal impossible to list all of the natural numbers however, owing to the fact that the list would be infinitely long. However many natural numbers you care to list I can still find one which you haven’t listed in much the same way as you can find real numbers which I have failed to list.
The only difference is that – again, you are methodical about your listing – the numbers I point out are not on your list are beyond the limit of the list rather than between numbers which are already included in the list.
Al: Of course it would take me forever to physically list all the natural numbers, but that’s not exactly what “list” means here. Instead, “list” means “give a rule for generating a list that will eventually get around to any given number.” In that sense, I can list the natural numbers with the simple rule “Name the numbers in their usual order”. Does this eventually get up to 17? Yes, after 17 steps. Does it eventually get up to 17,245,468? Yes, after 17,245,468 steps. And so on.
The integers and the rational numbers are listable by that criterion; I can specify “listing rules” that will eventually produce every given one of them. For the reals, that’s impossible.