Last week I posed this problem:

Several commenters did a wonderful job of explaining the answer. Let me just add a few words on the issue of “How can Tuesday be relevant?”
If the Tuesday part weren’t there, the problem would be easy. With two children, there are three equally likely ways to have (at least) one boy: The children in birth order might be Boy/Boy, Boy/Girl, or Girl/Boy. That gives a 1/3 chance of Boy/Boy.
So what does “Tuesday” have to do with it? Answer: Having (at least) one Tuesday boy is a lot more likely when you’ve got two boys than when you’ve got only one. So among those moms with a Tuesday boy, the Boy/Boy moms outnumber either of the other types. The three possibilities aren’t equally likely anymore.
It might help to see a picture. To make the picture fit on this page, I assumed there are only two days in the week — Tuesday and Friday:
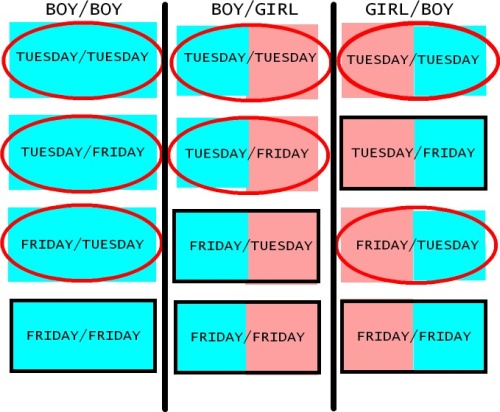
There are twelve ways to have at least one boy, and of those 12, there are 4 ways to have Boy/Boy. That, as we expected, is 1/3 of the sample. But now let’s focus in on the moms with a Tuesday boy. That eliminates half the moms in the second and third columns (leaving only those with red ovals around them) but eliminates only a quarter of the moms in the first column.
We’re left with 7 kinds of moms, 3 of which are Boy/Boy. So the probability our mom has two boys is 3/7.
With a seven-day week, you’ll have 49 rectangles in each column. The “Tuesday” condition leaves only 7 rectangles in each of the second and third columns, but leaves 13 in the first. So there are 13+7+7=27 rectangles altogether, of which 13 are Boy/Boy. The answer is 13/27.



Ok, that makes a lot more sense to me now. Thanks.
If the problem is changed to the one below, what is the answer?
A woman has two children, one of whom is a boy named Steven. What is the probability they are both boys?
It is interesting that if we continue to make the condition (boy born on Tuesday) more specific, then the probability will get closer to the ‘intuitive’ probability of 1/2.
If we know, for instance, that at least one of the children is a boy born at 1:03:23 AM on a Tuesday, then the probability that the other child is a boy is very close to 1/2. In this case, I believe the probability of two boys would be 1209599 divided by 2419199. (I might have made a mistake in the absolute numbers, but the general idea is correct.)
You left out your “more precision” definition of the problem.
This is critical in explaining how Tuesday matters:
“We gather all those women in the world who have exactly two
children, tell each of them to ‘Go home unless you have a boy
born on a Tuesday.'”
Without that, Tuesday is irrelevant. Every child has to be born
on some day. The fact that this particular one of hers happens
to have been born on Tuesday doesn’t matter in the original
statement of the problem.
For instance, say I flip two coins. One of them fell heads at
exactly 7 AM. What did the other coin show? If you pulled me
out of a group who got a heads between 7:00 and 7:01, the time
could be relevant. However, if you chose me in isolation, the
time would be as irrelevant as what I had for breakfast.
Ron:
For instance, say I flip two coins. One of them fell heads at
exactly 7 AM. What did the other coin show? If you pulled me
out of a group who got a heads between 7:00 and 7:01, the time
could be relevant. However, if you chose me in isolation, the
time would be as irrelevant as what I had for breakfast.
I’m not sure what “chose you in isolation” means, but I think that
on the most natural interpretation of the problem, the time is
very much relevant. Flipping heads at exactly 7AM is pretty
unlikely in any event, but it’s *less* unlikely if you flipped
two heads than if you flipped one. So this leads me to upgrade
my confidence that you flipped two heads.
(If “chose you in isolation” means that I asked you “at what
time did you flip one of those heads?” and got the answer
7AM, then I agree with you. If it menas that I asked you
“Did you flip one of those heads at 7AM?” then I disagree
with you.)
Using Mr. Landsburg’s simplified example, there are seven sets of qualifying siblings.
If we question the mom’s, 3 say they have BB, 4 say they have BG: 3:4 = 3/7.
But if we question the boys born on Tuesday, of which there are 8, 4 say they have brothers and 4 say they have sisters. 4:4 = 4/8 = 1/2.
Is this right? If so, from the original problem, how do we know whom to question, the moms or the Tuesday boys?
Ron: What you had for breakfast is irrelevant. A characteristic of the coin that showed heads that can be used to distinguish it from the other coin is not.
Suppose I tell you that I flipped two coins, and that one was tossed by my right hand and showed heads. If you believe that I toss all coins with my right hand, then the probability that both showed heads is 1/3. If you believe I always use a different hand for each toss, then the probability that both showed heads is 1/2. If, however, you believe that it was equally likely for me to make each toss with my right hand or left hand, then the probability that both tosses showed heads is 3/7.
If I tell you that one toss fell heads at exactly 7AM, and you believe there is a chance that the other coin could have fallen at a different time, then it matters. The exactly probability will depend on your statistical model for the times at which the other toss could have occurred. Different knowledge (and subsequent models) about the times at which I might toss coins will lead to different answers.
I keep spinning in circles on this one.
I get that you’re more likely to have 2 boys if you have a boy born on a Tuesday.
But aren’t you also more likely to have 2 boys if you have a boy born at all???
What if the question was that you have a boy born on day that isn’t Tuesday. I don’t get why that would or should or could change the answer?
And should the sum of all days equal 50% or 33% or something?
Apologies for triple posting but this is now driving me completely mad
I.G. Noranz: Is this right? If so, from the original problem, how do we know whom to question, the moms or the Tuesday boys?
The problem asks for the probability that a given mom in the sample has two boys. If the problem had asked for the probability that a given boy in the sample came from a two-boy family then we’d do your alternative calculation.
Dave:
But aren’t you also more likely to have 2 boys if you have a boy born at all???
Yes! For a random mom, the probability of 2 boys is 1/4. As soon as I tell you she’s got a boy, the probability of two boys goes up — from 1/4 to 1/3. Now when I tell you she’s got a boy born on a Tuesday, the probability goes up further — from 1/3 to 13/27.
Each new piece of information that is easier for 2-boy moms to satisfy, raises the probability that you’ve got a 2-boy mom.
Dave:
And should the sum of all days equal 50% or 33% or something?
No, it’s trickier than that, because some 2-boy moms have kids born on two different days and others have 2 kids born on the same day.
Dave-
Apologies, but this will likely make your head worse before (hopefully) clearing things up a bit.
A woman has 2 children, (at least) one of whom is a boy. From here, the probability that they are both boys is 1/3 (BB,BG,GB).
Suppose she tells you that her /first/ child is a boy. Now P(BB)=1/2 as GB has been knocked out of the sample space (BB,BG).
Suppose instead she tells you that her /second/ child is a boy. Now P(BB)=1/2 as BG has been knocked out of the sample space (BB,GB).
Now you realize, without her telling you whether her first or second-born child is a boy, that at least one of those cases must be true. You are either in the first scenario where P(BB) = 1/2 or you are in the second scenario where P(BB) = 1/2, so you conclude that P(BB)=1/2 before she tells you whether the first- or second-born child is a boy.
But, from the second sentence, this is obviously false because the probability is 1/3. The reason behind the mistake is that you can’t assume her answer is irrelevant. The fallacy here is akin to analyzing the Monty Hall problem, correctly concluding that you should switch doors, then switching /before/ the host opens one of the other doors. You paradoxically realize that the information has value, then choose to act before you have that information. Any new information about the children will change your estimate of the probability- but you need to wait until you have that information before you can make use of it.
Note: After she tells you that the first or second child is a boy, the probability that both are boys is exactly one half and not something slightly less than one half because there is no overlap- you can’t have 2 first-born sons (or at least it’s so absurdly improbabale that the probability is within an epsilon of 1/2).
Has this been empirically tested?
Skip the “in isolation” selection objection. I was
thinking of it wrong. That works only if you specify
order.
I did the same problem with coin flips. I’m going to
throw two coins, twice. The first flip, I’ll label
Heads or Tails. The second flip will further classify
the flip: Heads = Tuesday, Tails = Friday.
Now, I’ll tell you the result of the one of the two heats. I got
Heads with a Tuesday classification. What are the odds that I’ll
end up with two Heads? How does my weekday classification affect
the results?
Here’s the table of the 16 possibilities
for four consecutive coin flips. Remember,
every second flip is “day”. So, “Heads on
Tuesday” is a HH pair.
H H H H
H H H T
H H T H
H H T T
H T H H
H T H T
H T T H
H T T T
T H H H
T H H T
T H T H
T H T T
T T H H
T T H T
T T T H
T T T T
What can we eliminate?
T T T T impossible: I told you I got a Heads
T T T H
T H T H
T H T T
H T H T impossible: no Tuesday Heads
H T T H
H T T T
T H H T
T T H T
leaving:
H H H H 2 heads
H H H T 2 heads
H H T H
H H T T
H T H H 2 heads
T H H H
T T H H
Conditional chance of two heads, given
at least one is Heads on Tuesday: 3/7.
OK maybe I need to take a step back. If we know that one of her children is a boy, the chance of the other being a boy is 50%, not 33%. Is it?
It seems like the order of thinking makes a big difference. I kind of read the original question, given that “anything really”, then what odds that she sex of the other child is male?
Dave, there’s an ambiguity in the language here. “We know the sex of one of her children” could mean
1. There is a particular child of hers (eg the eldest) we know to be a boy
or
2. She has at least one son
In the former case, we know nothing of her other child so the probability is 1/2. But in the second case, there is no “other child”, because we don’t actually know the sex of either of her children.
Or to look at it another way. If we ask “is your eldest child a boy?” and we get the answer “yes” then we have eliminated half the possibilities (GB,GG) and left half (BB,BG) and of those 1/2 have two boys. But if we ask “are either of your children boys?” and get the answer “yes” we have only eliminated one possibility (GG) and left 3 (GB,BG,BB) of which 1/3 have two boys. And yet in both cases we could (ambiguously) say that we know the sex of one of her children.
Dave,
One important issue is easy to overlook, but it was clarified in the original problem statement. You need to take care in understanding where the extra information comes from, such as “at least one boy”.
If this information comes from asking a mother of two if she has at least one boy, then the probability she has two boys is 1/3.
If this information comes from asking a mother of two if her oldest child is a boy, then the probability of having two boys is 1/2.
If the mother enters a room and announces that she has two children and at least one is a boy, you have to ask yourself why and how she decided to tell you that. The likelihood with which you believe she has two boys will depend on your assumptions.
If you gather all women with two children and dismiss those with two girls (as in the original statement), then you have a probability of 1/3 for any of the remaining women to have two boys.
This issue is subtle and easy to be sloppy around. I’m sure I’ve been.
That seems so obvious now… >_<
Dave said “OK maybe I need to take a step back. If we know that one of her children is a boy, the chance of the other being a boy is 50%, not 33%. Is it?”
That sounds right, Dave. However, even though I haven’t followed all of this too closely, I believe Steve quoted “the probability of two boys” above, not “what is the chance that the other child is a boy.”
Great two-day week explanation, Steve. Before I saw it, the result seemed counter-intuitive or worse (wrong). Now it is obvious, dare I say trivial. Aha! How could I have been so dumb?
After having thought about this a while I think the correct answer is that the question doesn’t have enough information to get the right answer. The answer actually depends on how the woman was chosen.
If you start with the set off all women with two children, winnow the list down to only those with a boy born on Tuesday then ask the question the answer is 13/27.
If you pick a woman from the set of all women with two children and then ask her to randomly (fair coin) pick one child and tell you the sex and day of birth the odds that the other child is the same sex is 1/2. The odds they are both boys is 1/4.
In both case you know the sex and day of birth of one child but the odds are different because the mothers were sampled from differing sets of people. In particular, in the first case a smaller subset of all women with two children was used. The issue is not the information you know but whether or not that information was used to cull the sample set and hence bias the odds.
Stephen Coy: This is why, in the original post, I carefully specified the winnowing process.
In response to Andy’s question:
“If the problem is changed to the one below, what is the answer?
“A woman has two children, one of whom is a boy named Steven. What is the probability they are both boys?”
It becomes very nearly one half. Say there are 1000 names, each of which is equally likely for a boy. Consider the scenarios in which she has at least one boy:
If a woman has two boys, there are 1000 x 1000 possible name pairs, of which 1000 + 999 include at least one steven (1000 cases in which boy one is named Steven plus 999 cases where boy two is named Steven and boy one is not). The likelihood of having a boy named Steven if she has two boys is therefore 1999/1,000,000.
If a woman has one boy and one girl, there are 1000 (# of boy names) x (However many girl names there are) possible name pairs. Within this set of name pairs, for each girl name, there is one name pair in which the boy is named Steven. So the likelihood of having a boy named Steven if the woman has a boy and a girl is equal to (Girl names) / (1000 x (Girl names)), or 1/1000.
The total chance of a two-child woman with one boy having one boy named steven is the chance that she has two boys, one of which is named steven (1999/1,000,000), times the chance she has two boys (1/3) PLUS the chance that she has a boy and a girl, with the boy being named steven (1/1000), times the chance that she has a boy and a girl (2/3). This equals .001333. The share of that probability that comes from a situation in which she has two boys is 1999/1,000,000 * 1/3 = .000666333, or about 49.7%. Thus if you know she has two children, one of which is named Steven, there is a 49.7% chance she has two boys.
As you substitute more and more specific traits for the “born on Tuesday” element of the riddle, you get closer and closer to an answer of 1/2 as previous comments have mentioned. This is because you increase the ratio of the chance of attaining that outcome with two boys to the chance of attaining that outcome with a boy and a girl.
The only reason having two boys instead of a boy and a girl doesn’t double your chance of having a boy with a given trait is because there is a certain likelihood both boys will have the trait. In other words, adding a second boy doubles the probability of achieving the trait ONLY if the first boy doesn’t already have the trait, so you can add the probability of the second boy having the trait, but you have to subtract the probability of both boys having it. When you’re considering an extremely rare trait, the chances of both boys having it is miniscule and you are essentially twice as likely to get the trait at least once if you have two boys.
You can think of this one other way: the rarer a trait is that you know, the more likely you now know something about a SPECIFIC child (i.e., the less likely it is that you have learned something that is true of both children). Thus the problem becomes more like the alternative formulation where you know the woman’s first-born is a boy.