The most fun you can have on the Internet is to find a beautiful, succinct argument with a conclusion so unexpected it seems like magic. For today’s fun, I am indebted to Michael Lugo, at God Plays Dice.
Lugo’s original post is so good it seems almost superflous to paraphrase it, but I can’t resist the temptation.
Drill a tunnel through the earth, from anywhere to anywhere — New York to Maine, or New York to Australia, or wherever else you like. Like so:
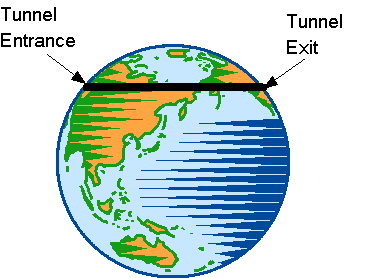
Now drop the object of your choice (Lugo suggests a burrito, but you might prefer a gravity-driven train) into the tunnel entrance and wait till it comes out the other side. It’s a standard calculus problem to calculate how long you’ll have to wait: The answer is 42 minutes, regardless of the length of the tunnel. I’m sure I once found it surprising that the tunnel length doesn’t matter, but I’ve known it long enough that I now take it in stride. So that’s not how Lugo surprised me.
The surprise is that if you change the size of the earth (while maintaining its density), the answer is still 42 minutes. Whether the earth is the size of a pea or the size of the solar system, it’s a 42 minute trip from one end of the tunnel to the other. (We’re — quite reasonably — ignoring the effects of relativity here. For an earth that was half the size of the universe, we’d have to make some corrections.)
Why so? You could, of course, discover this through a direct calculation. But Lugo provides a much slicker argument, namely:
Once you know that the travel time is independent of the tunnel length, it’s clear there are only three things it can depend on: The earth’s density, its radius, and the gravitational constant. Neither density nor radius have anything to do with time, so we’re really going to have to use that gravitational constant, which is measured in units of
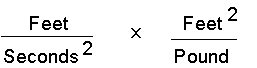
(The first factor is the 32 feet per second squared that you learned about in elementary school; the second factor depends on distance from the center of the earth and the mass of the earth, neither of which varies in those elementary school problems, so it’s never explicitly mentioned.)
If you multiply that gravitational constant by density (which is pounds per cubic foot), you’ll get a bunch of cancellation, leaving you with
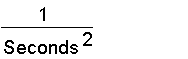
Now you’ve got something that depends only on time! To turn this into an actual number of seconds, you can just invert it and take the square root. At that point, you’re done! (Except maybe for multiplying by some dimensionless constant.) Any attempt to bring the radius of the earth into the formula is going to introduce units of length, which have no business popping up in a formula for time. Therefore the earth’s radius must be irrelevant.
Isn’t that cool? And amazing?
(And yes, there are hidden assumptions, e.g. that the solution must be not just a function of mass, length and the gravitational constant, but a rational function — so this is not quite a proof, but a highly convincing heuristic argument that does give the correct answer. That, I think, in no way detracts from its coolness.)
Lugo’s post is both more concise and more carefully worded, but I thought this slightly longer and less formal version might be helpful to at least a reader or two. Besides, I felt like writing it.
Do you have an equally amazing argument to share?



Thats awesome!
Here is (what I imagine to be) a stupid question.
Surely this only works when the tunnel goes through the middle of the earth? rather than cutting the top as your diagram shows? Wouldn’t gravity drag the item to the side otherwise and it bounce around?
Also, does this imply something about the speed of a collapsing star? Only density would matter, rather than size?
Dimensional analysis is a wonderful thing. It should be taught in the opening chapter of every physics textbook.
@Nick – yes, this assumes you put the burrito on a frictionless rail/elevator or something similar.
As for the collapsing star, the really cool argument starts from the known fact that the time taken through the tunnel is independent of the tunnel length. I’m don’t know, off the top of my head, any similar amazing symmetry of the dynamics of a collapsing star, but if you do, let’s hear it :-)
The poem is terrible, but the intent is clear.
http://www.straightdope.com/columns/read/113/the-story-of-schroedingers-cat-an-epic-poem
42, eh. Now that rings a bell.
Interesting outcome, but to nitpick: standard Earth gravity is a bit over 32 ft/sec^2, not 16.
Unexpected?? It is after all the answer to life, the universe and everything.
Martin: Fixing this now! Thanks for the catch.
I don’t understand the argument that the time can’t depend on the radius. With a larger radius, the burrito would move closer to the center of mass more slowly … why could that (intuitively) not affect the travel time?
@Phil If you change the radius of the earth, but keep the mass constant, then yes, the burrito moves more slowly. If you change the radius of the earth but keep the *density* constant, the higher gravity makes the burrito move faster at the start, and it takes the same time even though it has further to go. This all assumes that the earth has constant density throughout.
Mike H,
The burrito doesn’t necessarily have further to go. It’s (say) 1000 km regardless of the radius of the earth.
By Dr. Landsburg’s exposition, we accept that the time is the same regardless of length, for a fixed radius of earth. Now, how do we intuitively get to the argument that the time is the same for any radius?
Dr. Landsburg says, “… radius [does not have] anything to do with time.” That’s the part I don’t understand. Why is it so easy to argue that radius has nothing to do with time?
In SI units g is quite close to 10 (9.8 m/s2), which makes rough calculations simple.
The 42 minutes thing is quite suprising at first, but does make sense – like the period of a pendulum being only dependent on the length and g, however large the swing.
That’s interesting.
The fact that the earth’s radius is irrelevant can also be seen to be true from the following logic:
1) If, instead of dropping the object from the surface of the earth, you first burrow X miles into the tunnel and drop if from there, the time it takes to reach the point X miles from the end of the tunnel on the other side must be 42 minutes (i.e. the same as if you did not burrow at all). This is because the object’s motion is simple (simply?) harmonic, and for simple harmonic motion, the amplitude is irrelevant. E.g. to take another example, if you make a pendulum from a string and a rock, the time it takes the to go from one side to the other is not dependent on how high the rock swings on either side (roughly speaking, and assuming amplitude is not too high)
2) To modify 1) slightly, once you burrow X miles into the tunnel, you might as well ignore all of the earth’s mass that is farther from the center than you are — this mass is totally irrelevant to your motion. Thus, you might as well be performing the same experiment on a smaller planet to begin with — and therefore the radius of the planet is irrelevant.
Admittedly this line of reasoning is not as cool as Lugo’s, but perhaps it is the 2nd coolest way of proving the radius is irrelevant.
> This is because the object’s motion is simple (simply?) harmonic, and for
> simple harmonic motion, the amplitude is irrelevant.
The motion is harmonic because the force on the object is proportional to the distance from the tunnel’s middle point.
Jonathan Campbell:
Admittedly this line of reasoning is not as cool as Lugo’s,
I’m not sure I agree with that. It’s pretty cool.
Jonathan Campbell: Outstanding. I like that explanation.
Nick: “Surely this only works when the tunnel goes through the middle of the earth? rather than cutting the top as your diagram shows?”
No, it does not have to go through the center of the earth. That’s what’s so cool about it.
I think the friction coming from the air would be a far bigger problem. Of course, in an evacuated tube…
“… radius [does not have] anything to do with time.”
He means, radius is measured in metres/inches/furlongs, time is measured in seconds/years/fortnights.
Radius is a measure of length, with no time units. The only way it could inform a measurement of time is by combining it with another quantity that involves time and length (eg, speed).
Something from rock climbing that I think is pretty counterintuitive:
A “main anchor” can be built by attaching rope to two independent anchors, and then joining those two pieces of rope together at a point below both anchors. The purpose of this is to share the load between the two anchors. (Simplified)
The angle at the main anchor determines the percentage of the load that each anchor bears.
-At 0 degrees, each anchor bears 50% of the load.
-At 60 degrees each anchor bears about 58% of the load.
-At 120 degrees each anchor bears 100% of the load, and above 120 degrees each anchor bear GREATER than 100% of the load.
I find it pretty counterintuitive that with a load of X on a main anchor, it is possible to rig the two individual anchors such that they each share a load of greater than X.
Hope that explanation made some sense. If not, check out Wikipedia on climbing anchor equalization.
Mike H,
If you drop a paperclip, how long it takes to reach the earth depends on the radius of the earth, the density of the earth, and how high you hold the paperclip before dropping it. None of those have time units either, but the argument “therefore it doesn’t matter how high you hold the paperclip” is invalid.
However, the gravitational constant does have units of time in it, Phil.
Sameer,
True! That’s my point. Even though it’s G that has units of time in it, you still need the radius of the earth, density of the earth, and height of the paperclip to determine how long it takes to fall.
So I don’t understand the argument that you don’t need the radius of the earth or density of the earth to know how long it takes for the burrito to travel.
I’m obviously missing something, since everyone agrees the original argument works. I just don’t know what it is that I’m not understanding.
If the tunnel doesn’t go through the centre of the Earth why won’t the object get stuck at the point closest to the centre? Are you assuming a vacuum?
Robert Wiblin: Momentum carries it through to the other side. (Ignoring friction.)
hmm…i wonder if the burrito will still be edible with the heat inside the mantle of the earth XD…