In 1706, the British astronomer John Machin calculated π to 100 digits (by hand of course). His trick was to notice that π = 16A – 4B where A and B are given by
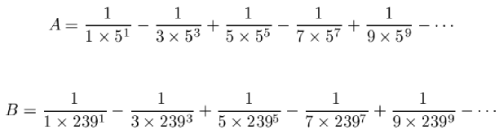
If you’re computing by hand, this is an excellent discovery, because the series for A involves a lot of divisions by 5, which are a lot easier to calculate than, say, divisions by 7, and the series for B converges very fast, so just a few terms buys you a whole lot of accuracy. (Try using, say, just the first four terms of A and just the first term of B to see what I mean.)
Machin’s 100 digits were a substantial improvement over the 72 digits obtained just a little earlier by Abraham Sharp, using the far less efficient series
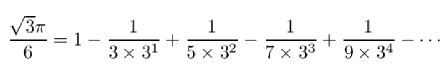
In 1729, a Frenchman named de Lagny got all the way to 127 digits, but, in the words of the scientist/engineer/philosopher/historian Petr Beckmann (of whom more later), de Lagny “sweated these digits out by Sharp’s series, and so exhibited more computational stamina than mathematical wits.”
Machin’s methods were ingenious, but no more ingenious — and certainly no more striking — than John Wallis’s 1655 discovery that
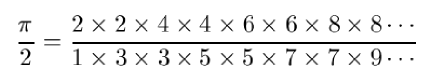
which still looks awesome to me after decades of familiarity.
The history of π closely tracks the history of human ingenuity — and not infrequently of human folly as well. Where there was freedom, there was progress. Where there was tyranny, there was stagnation. The best place to read all about it is Beckmann’s wonderful book A History of Pi, which is the tale not just of the π-hunters and their ideas, but of the times in which they lived, and the world they helped to make, and the broader trends that allowed science to flourish. If you don’t already own it, you’re in for a treat. Happy Pi Day.



It’s “Petr” Beckmann.
Paul Sand: Fixed! Thank you.
Question: Could you rephrase the last equation as “the absolute value of the product of all the even numbers (except zero) divided by the product of all the odd numbers?”
Have you read this paper:
http://www.math.utah.edu/~palais/pi.pdf
Steve Friedman: Well, not quite. First of all, each even number appears twice, and so does each odd number. Second, it matters what order you do your multiplications in. If you start by multiplying out the entire numerator, you’ll never finish. Instead, you need to break this up as (2/1) x (2/3) x (4/3) x (4/5) x …. . Then if you stop after, say, the first few hundred terms, you’ll have a pretty good approximation to π/2 , and if you stop after a few thousand you’ll have an even better one. There’s no limit to how good these approximations get if you go far enough.
Does this mean that building plans in which pi is used for calculations will fall if the ninety-nigh or one-hundredth position is off? Don’t most engineers settle at 3.14159?
Eric, I don’t think building buildings is exactly precision engineering. Considering that carpenters and construction workers generally don’t bother with measurements more precise than 1/16th of an inch, more than the first couple of digits of pi aren’t going to matter to them.
Engine builders, however, are going to need quite a bit more precision when designing the pistons, lest the engine fail or be horrifically inefficient.
To get an idea of what the digits of pie get you, each decimal gets you around an order of magnitude of precision (it varies).
So a builder building a 100 foot arch using 3 to calculate the circumference is going to be off by about 14 feet – not good. But at 3.1 he’s only off by 1.3 feet, which might be good enough. At 3.14 he’s only off by half a foot, so that’s probably plenty accurate in most circumstances. At 3.14159, he’s only off by a touch more than 1/1000th of an inch, and is probably accurate enough for even the most extreme skyscrapers being built. That’s also probably good enough for the engine pistons, but you wouldn’t want much less accuracy than that, and that might not be anywhere near precise enough if you’re trying to build an atomic clock or an atom smasher.
It all depends on what you need it for.
Tau/2 day you mean?
Bigjeff5,
This isn’t to deny what you write. I read that in 1840s, Sam Colt and others did something to that time considered: They created interchangeable parts. These were eventually shown to astounded weapons manufacturers in England at some exposition. Prior to that time, muskets were crafted manually, and each bolt was created to fit exactly.
The tolerances of pistons, cams, transmission and differential gears may go to a few more decimal places, but making something so exact as to render that something available for only one purpose is not economical. Thank you, though, for showing how the gaps in a bridge span (arch span) diminish with just a few more decimal places.
Just so you know, my Dad was a Civil Engineer, designing bridges and other structures. Years ago, I had mentioned to him that someone calculated pi to 32 decimal places and he was the one who asked me if the building would fall because he used 3.14159. I’m not that clever, so blame him.
Do you know where to find proofs of these identities? If it’s 17-18th century math I might just understand them.
Martin-2: Machin’s formula is quite easy to prove as long as you know some basic trig identities and the Taylor series for the arctan function. The Wikipedia page here is a perfectly good reference.
Steve (11): Thanks! Well, I know some basic trig identities so we’ll see how this goes.
Off topic: From time to time we chide Krugman for saying things that seem not merely poorly supported, but actually contrary to economic principles. Thus I’d be interested in people’s take on Mankiw’s column,
When the Scientist Is Also a Philosopher.
At the outset, Mankiw acknowledges that economist columns inevitably reflect political perspectives. And then he argues that economic advice should be offered with humility. I find both insights to offer a refreshing bit of candor.
But then Mankiw goes to his own political perspective: “That is why we economists should be sure to apply the principle ‘first, do no harm.’”
Can you think of a worse bit of insight regarding economics — especially following an exhortation to humility? If we’re humble, we must acknowledge that we pretty much can never foresee all the consequences of our actions. Thus, the adage “first, do no harm” is an adage for radical inaction.
Hell, even physicians don’t subscribe to this adage. A surgeon who was motivated to avoid causing any harm would never make the first incision into a patient. A physician would never prescribe a drug with side-effects (which is most of them) – or that might have side effects (which is the rest of them). Etc.
I’d expect an economist, of all people, to acknowledge that there are costs and benefits of pretty much any course of action. Humility should prompt us to acknowledge that our knowledge of, and ability to forecast, outcomes is and will always be incomplete. But the choice to avoid unanticipated consequences through inaction comes at a cost – just as any other choice does. The game is not to avoid harm. Rather, the game it to optimize some function that involves avoiding harm, minimizing expected harm, achieving benefits, maximizing expected benefits, etc. “First, do no harm,” is among the most facile – and common – bit of bad advice to ever circulate. It’s especially bad when coming from Mankiw’s pen.
We now return you to a discussion of Pi, already in progress….
“Do no harm” is just “laissez faire” by another name.