In high school, we used to play four-dimensional tic-tac-toe. The board looks like this:
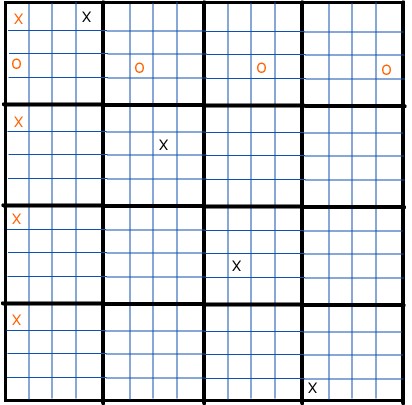
Here each four-by-four subsquare is an ordinary tic-tac-toe board (except that it’s four-by-four instead of the traditional three-by-three). You should think of the four subsquares in the first column (or any other column) as stacked above each other in the third dimension. The red x’s form a vertical line in that direction, so if you manage to place four x’s in those positions, you’re a winner.
You should also think of the four subsquares in the first row as stacked above each other in yet another dimension. The red o’s form a diagonal line passing from the bottom left to the top right (using “bottom” and “top” to refer to directions in this fourth dimension). And the black x’s form another kind of diagonal line, passing from one corner to another through all four dimensions. So there are a lot of ways to win this game.
In ordinary (two-dimensional, three-by-three) tic-tac-toe, two smart players will always battle to a draw. If you extend that game to four dimensions (so you’ve got nine three-by-three subsquares), the exact opposite is true: No matter how smart or dumb the players may be, someone always wins; draws are impossible. What about the larger four-dimensional game I’ve drawn above? Is there a winning strategy in that game? I’ll let you ponder that.
I hadn’t thought about four-dimensional tic-tac-toe in many years. Now it’s much on my mind, because a problem about higher dimensional tic-tac-toe may be ushering in a sea change in the way mathematical research is done. I’ll tell you more about that before the week is out.



I’m going to guess that it’s something like the first player to move always winning. If I remember correctly, that was the case with 3x3x3 games. I found that out the hard way when the A* algorithm I coded up for my undergrad AI class would essentially panic whenever asked to go second. I mention that because I have a feeling the sea change you’re talking about is using computerized search and proof mechanisms.
(Actually now that I think about it may not have been A*, but it was something like that.)
I remember a old computer game that was 3-d tic-tac-toe game on a 4x4x4 board. I thought about this at some point in college and managed to convince myself that 5x5x5x5, 6x6x6x6x6 etc boards (side length n+1 in dimension n), where interesting games in the some sense. If I remember right I think it (my conjecture) was that the 1st player can always win on other kind of board (I assumed it was regular in the sense that 3×4 boards didn’t count, but what is a diagonal there anyway).
You can play against another person or a computer program (that is quite good) here: http://www.ugcs.caltech.edu/~willsmit/4d/index.html
Pretty fun!
My guess is that it has something to do with the relationship between the number of ways of winning and the number of blocking opportunities. On a 2D 3×3 board, the best opening move is in the middle, and there are 4 ways of winning through the middle square. The second player has 4 moves, so he or she can, if playing correctly, always place the O to block a win.
In a 4D 3x3x3x3, I think there are (if I counted right) 40 ways of winning through the middle square. If X takes the middle square, he or she should not only always be able to win, but always win by the 5th move.
I haven’t extended to 4x4x4x4 yet, but it seems likely that the ratio of winning paths to blocking moves is less than for 3x3x3x3, since the number of winning paths should be the same (40).
when you ladies are done playing tic-tac-toe, give the 4-d Rubik’s cube a try
;)
http://www.superliminal.com/cube/cube.htm
What’s the algorithm for the number of winning lines? In a 3×3 square, there are 8 lines. In a 4×4 square, there are 10. In a 3x3x3 cube there are 76? 8 in each of 9 faces, plus 4 diagonals. Obviously, the algorithm needs to include the side length and the number of dimensions, but I don’t see it.
If you have been playing 4D tic tac toe against a friend (who happens to be a physicist who studies string theory) you may want to buff up your understanding of higher dimensions. I really like this video and I think it breaks it down into to sufficiently easy to understand ideas:
You may still lose to your friend but at least I think you’ll enjoy the video.
In the science museum La Villette in Paris, they have this 3D tic tac toe, composed of a very big a 4x4x4 (or 5x5x5 cant remember) structure with nodes that can light up in the colors of each player. You play by typing in the coordinates of a node on a control panel in front of the 3D structure causing the node to light up.
Remeber playing this as teenager , was great fun. But then the whole structure just reset in the middle of a game – guess they wanted other ppl than me and my friend to use it.
I think this game is known to be a win for the first player.
See the following article:
“Qubic: 4 × 4 × 4 Tic-Tac-Toe”
Oren Patashnik
Mathematics Magazine, Vol. 53, No. 4 (Sep., 1980), pp. 202-21