I’m eager to summarize the (largely excellent) discussion of last week’s nightmares and to talk about what it all means. I’ll surely get to that in the next few days. But meanwhile, we have another loose end to tie up.
I recently asked what comes next in the following series:
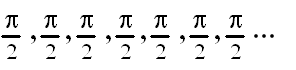
The answer, of course, is

Please raise your hand if you found this intuitively obvious.
In case your hand didn’t go up, consider the following sequence:
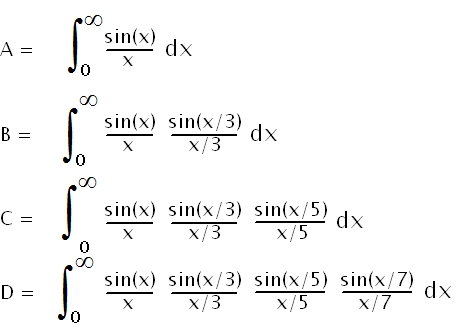
And so forth.
Next time you’re stuck on an airplane, you can amuse yourself by attempting to prove that
Roughly the reason for this is that each integral represents (in a non-obvious way) the intersection of two areas X and Y, where X is the same area for each integral but Y shrinks a little each time you move down the list. Initially X is contained entirely inside Y, so the interesection is just X. This remains true as Y shrinks, and shrinks, and shrinks again, but eventually Y shrinks enough so that it no longer contains all of X, and that’s when the integrals start shrinking.
Fun fact: After this was discovered by David and Jonathan Borwein, Jonathan verified that the computer algebra software package Maple reports the correct values for all these integrals — and then, as a practical joke, reported this to Maple as a “bug” in the software. Maple computer scientist Jacque Carette reports that “I must have spent three days on this project before I figured out that Jon had tricked me”.
More here.



Thanks for explaining in such a clear way – I can understand how this could happen.
One could also argue that an infinite list of pi/2 would fit your initial description, so I am not sure about the “of course”.
Jonathan Borwein has an evil sense of humour.
I gather not many flowers were sent to Jonathan’s funeral?
This has all the problems everyone pointed out ahead of time. There is nothing in the original problem which enables the reader to conclude that you wanted the above algorithm rather than the algorithm “pick pi/2 every time”.
“Guess which algorithm I had in mind, with no information” isn’t an IQ test, either.
@Ken
Maybe it’s some kind of math standard/notation/representation that we don’t understand that makes this question and answer obvious? For me it was like asking 2+2=? without defining what +,=, or ? means. I figured I was just ignorant of this type of math and moved on.
Never mind, I get it now. I just didn’t read all the way to the end (H=…).
Whatever Steve.
Geez…. you guys need to get a sense of humor!
[Sorry, I normally love the commenters on this site, but this time they all seem oblivious to the fact that SL was making a joke in order to introduce this awesome math fact.]
@Scott H and Ken Arromdee:
You guys are not amongst the ones I expected to be caught in this little trap but …
Steve was joking. He found a strking result in calculus. A nice little sequence that looks so innocuous, each one comes out exaclty 1/2, pattern looks predictable *yawn* and then suddenly this whacked out number amazingly close to 1/2 but not 1/2 pops up. He is highlighting the sheer goofy delightfulness of it. That’s why he said the next term ‘of course’ is … because ‘of course’ is wildly inapt. That’s the joke.
Here endeth the lesson.
@CC: A goodly number of us got it; there some amusing stuff on the original thread. Of course on that thread I even explicitly explained the joke, and still …
@Ken B: Got it, thanks.
This reminds me: I think SL should do a post on how to prove various functions don’t have indefinite integrals (in terms of elementary functions).
But then I also think he should post about what large infinities have to do with the power of various proof systems, and…. well, I could keep him busy for a while.
@CC: there are by actual count 407 posts arguing that the Peano Axioms are consistent. They all have *lots* of dissenting comments.
I can recommend a book on large cardinals and proof systems — Stillwell, Roads to Infinty
Me, I’d prefer less math, more econ.
Forget about understanding the math. I want to understand how people type blog comments with their hands raised.
@nobody.really: No you don’t. Trust me.
A nice review of the sinc function.
LOL!
I think there’s an object lesson in extrapolation as well. Here we have some data points, and we’re trying to discover the underlying reality. Nearly everyone’s intuition about the underlying reality is wrong.
It’s been a while since I ran a mathematical proof by induction, but this seems to have a good chance at tripping up undergrads.
Steve, the ‘Mike H’ above (“A nice review of the sinc function”) is not me. And it looks like spam.
Mike H: Yes, I see that it’s not you, but I’m disinclined to think it’s spam, since the word “sinc” does not appear in the post, and few spammers would have taken the time to discover that the function sin(x)/x is often called the “sinc” function (few, indeed, would even have glanced at the post).
Apologies to the original Mike H. The sinc function isn’t intentional spam, but a clumsy hat tip to Dr. Landsburg’s very cool combination of sin(xN)/xN functions presented in a deceptively simple package.
Not nice, submitting a bogus bug report :) and remarkably I remember just… enough… calculus… 25 years later that I can get the joke. :)
Your text is misleading because the 3 dots don’t usually denote a missing number but an infinite series.
http://en.wikipedia.org/wiki/Lagrange_interpolation
Coming from a signal processing background, the sinc function suggests the Fourier Transform of a ‘top hat’ function. Knowing that multiplication in one domain corresponds to convolution in the transformed domain and the definate integral is given by the value of the tranform at zero helps. I convolved top hat functions 1, 1/3, …, 1/15; the value at zero reduces when 1/3 + 1/5 + … + 1/15 exceeds 1. (Pictures would help the explanation).
Joe M.: Yes, this is exactly what’s going on.
Steve, Can you confirm if there’s just one solution to this series viz. Can ‘H’ be anything other than the large number you have said it would be ?
Denzil: Another possible solution is 62.
https://xkcd.com/217/
:)