 My mother, who reads this blog, reports that she’s lost a few nights’ sleep lately, tormented by thoughts of Knights, Knaves and Crazies. Serves her right. Once when she and I were very young, she tormented me with a geometry puzzler that I now know she must have gotten (either directly or indirectly) from Lewis Carroll; you can find it here. If she remembers the solution, she should be able to sleep tonight.
My mother, who reads this blog, reports that she’s lost a few nights’ sleep lately, tormented by thoughts of Knights, Knaves and Crazies. Serves her right. Once when she and I were very young, she tormented me with a geometry puzzler that I now know she must have gotten (either directly or indirectly) from Lewis Carroll; you can find it here. If she remembers the solution, she should be able to sleep tonight.
Herewith, a proof that a right angle can equal an obtuse angle. The puzzle, of course, is to figure out where I cheated.
But wait! Let’s do this as a video, since I’m starting to fool around with this technology and could use the practice. Consider this more or less a first effort. If you prefer the old ways, you can skip the video and read the (identical) step-by-step proof below the fold.
Or, if you prefer to skip the video, start here:
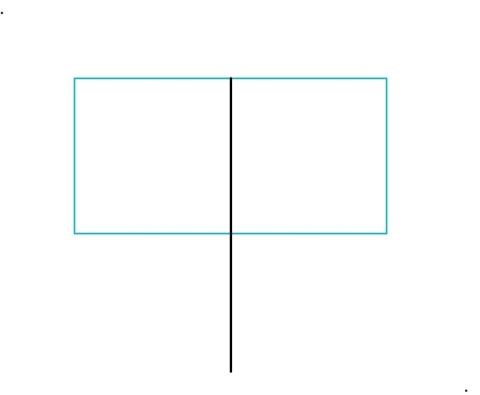
1. Draw a rectangle:

2. Bisect the horizontal edge of the rectangle, and continue the perpendicular bisector downward:
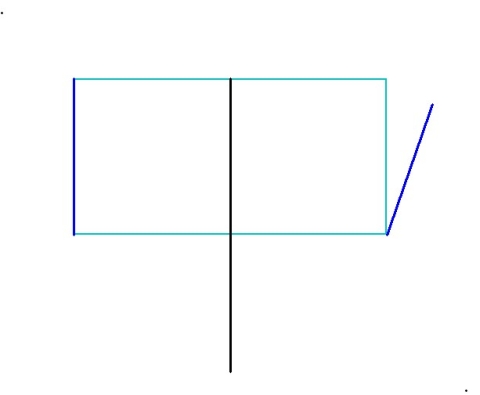
3, Attach, at the bottom right-hand corner, a line segment as shown, and exactly equal in length to a vertical side of the rectangle. I’ve colored the new segment and one of the vertical sides dark blue as a reminder that their lengths are equal:
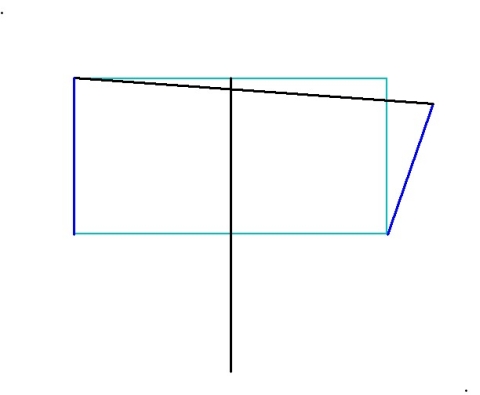
4. Connect the tops of the two dark blue segments:
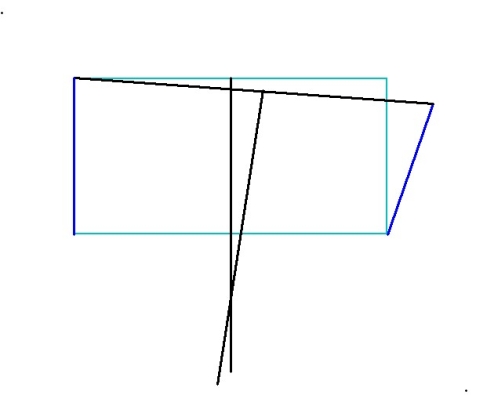
5. Bisect the line you just drew, and continue the perpendicular bisector downward:
6. Add the two red lines as shown. Notice that these red lines are two sides of an isoceles triangle, hence equal in length.
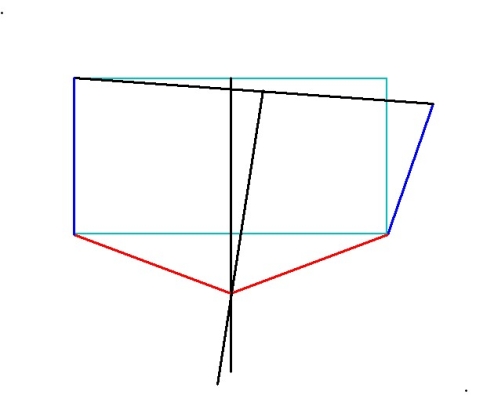
7. Continuing to focus on that same isoceles triangle, let’s mark the equal angles with double arcs:
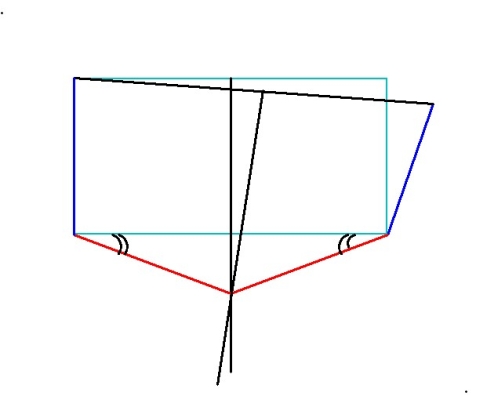
8. Add the green lines as shown. Notice that these are also two sides of an isoceles triangle (because they meet on the perpendicular bisector of the triangle’s “base”), which we’ll remember because they’re the same color:
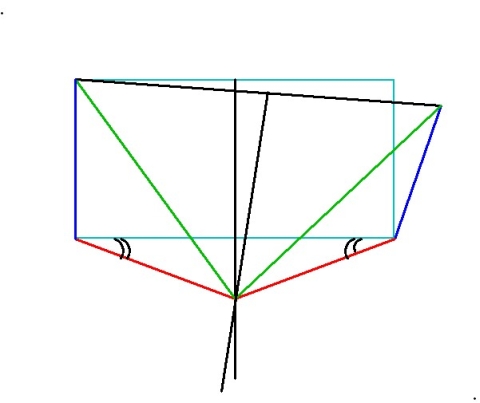
9. Now we’ve got two blue-green-red triangles, one on each side of the diagram. The two blue sides are equal, the two red sides are equal, and the two green sides are equal, so the triangles are congruent. Therefore corresponding angles are equal. Let’s mark the corresponding blue-side-to-red-side angles with single arcs to remind ourselves they’re equal:
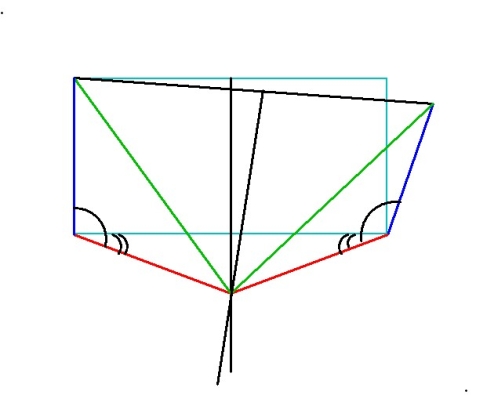
10. Okay, the two single-arc angles are equal. So are the two double-arc angles. On the left side, if you subtract the double-arc angle from the single-arc angle, you get a right angle. On the right side, if you subtract the double-arc angle from the single-arc angle, you get an obtuse angle. Therefore a right angle and an obtuse angle are equal.



I don’t know if this is part of the “cheat” but how do you know the two perp bisectors meet outside the rectangle? The red triangle might be upside down.
Spoiler Alert :
I have tried to make my answer invisible : if it worked, you can read it by selecting the text between here…..
Your right-hand triangle should be flipped over.
….. and here.
I think the “cheat” is on step 9. You state “The two blue sides are equal, the two red sides are equal, and the two green sides are equal, so the triangles are congruent.”, but I don’t think this is correct, I do not believe that the two green sides are equal.
(Spoiler: solution follows)
What Mike H said — specifically, you can show that when you draw the slanted perpendicular bisector in step 5, and extend it until it meets the original black vertical line, it will actually meet *so* far down, that the right-hand green line added in step 8, will pass *below* the bottom-right corner of the right-hand blue square. (Not above it, as you drew in the picture.) Thus the right-hand triangle will be congruent to the original, but it will be in the same orientation, not a mirror image as drawn in the diagram.
In your drawing you fudged the length of the right-hand blue line in step 3 and the angle of the perpendicular bisector in step 5, to make sure it wouldn’t come out that way :)
I’m not sure I like a “puzzle” that boils down to egregiously distorting angles/length and framing it as “new video software” and “my drawing skills are limited by my shaky mouse”.
But it’s good to spend a few minutes wondering if there’s something tricky about congruent triangles…
It might serve as a proof that the right tirangle can not be constructed. We don’t easily see how far the intersection of the two bisectors is. So we don’t know whether the right green line goes above or under the lower right corner. The construction show that being above the lower right corner leads to contradiction.
#2 Your tags didn’t work, but at least the rest of the post has not become invisisble!
Fun puzzle. I could see that the angle of that perpendicular was wrong on the diagram, but failed to follow through to see the consequences.
Robert Easton (#1): Try drawing it with the bisectors meeting inside the rectangle. You’ll still get exactly the same conclusion (though you’ll have to add angles at the end instead of subtracting them).
Before doing any calculation, the only possibility I see is that the two perpendicular bisectors should intersect inside the rectangle, not outside.
Is one of the angles equal to The Multiplier?
Martin (#9): See #8.
Steve –
Comment on the technology: on my machine, it was hard to distinguish between the dark blue lines and black lines in the video, although in the still images I can see the difference easily.
Mike H (#2): Whatever you did didn’t work, but I fixed it for you.
#13 – It is really fun now! I highlighted it a few times just for amusement value. Simple things.
I see two cheets: the blue line in step 2 is shorter than a side of the rectangle, and the bisector in step 5 is not perpendicular to the connector from step 4. If they had, the triangle would be flipped, as Bennett points out in #4.
If we call the angle between the blue line and the side of the triangle A, then angle between the red line and the bottom of the triange (let’s call B) would be 90 – A/2. If say, A is 30 degrees, then B is 75 degrees. At that angle, the two perpendicular lines would intersect at nearly twice (1.866 times) the length of the bottom edge of the rectangle below the bottom.
To get the red line so close to the bottom of the triangle, the line between the blue line and the rectangle would need to be almost a continuation of the bottom edge, perpendicular to the side.
To elaborate on what Mike H and Bennett Haselton have already said, here’s a sketch, with enforced correct proportions/angles/etc, of all the places the incorrectly drawn green line *could* have been, based on how far you rotate the original right edge of the rectangle: http://imgur.com/8gMC4SM
As they observed, it’s never inside the original rectangle.
Here, I hope, is a proof that my solution (#2) is correct (requires Java, didn’t work on my machine):
http://www.geogebratube.org/student/m43286
If the link above doesn’t work, try http://www.geogebratube.org/student/m43286?mobile=true
Try dragging points E or B. Sorry, Steve, for using up lots of comment numbers!
That right hand triangle is like potential GDP?
I admit, I had to get out a piece of paper and a protractor to prove to myself what Steve had done, though my eyes were good enough to see immediately that something was off in the drawings he provided.
Very Nice, Mike H.!
Appears in “Fun With Mathematics” by J S Meyer (1952). “Fallacies” chapter, number eight, page 156.
I owned this book when I was a kid. Good fun and instructive. Chapters like “how to make a slide rule” and “number systems other than ours”.