It’s said that Pythagoras had a man put to death for blabbing in a public bar that the square root of two is irrational. Today I hope I can post this without fear of reprisals. I don’t know who first drew this beautiful proof, which works equally well in modern English and in ancient Greek:
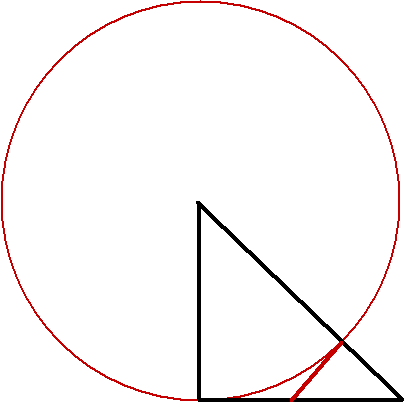



Hmmm, let’s see if I can remember this. We’re assuming that the square root of two is A/B reduced, so the black triangle has legs of A and a hypotenuse of B. That’s the smallest isosceles triangle having three integer sides. But the lower-right triangle is also isosceles and also has integer sides (hypotenuse A – B and legs 2B – A), and it’s smaller. (The red line has length equal to the right small black line because it’s an isosceles triangle, and equal to the lower-left black line because they’re both tangent to the circle.)
I did finally get this but I confess not immediately. *spoiler alert* the construction shows an infinite regress, but why does that suffice? The idea is that irrational refers to incomensurable lengths. If rt2 is rational then some integer number of rt2 lengths will match some other number of 1 lengths. So there will be a triangle, the big one here, where all sides are integer length. Use those two “some integers”. But then you construct a smaller one by drawing a smaller circle. (The sides are equal by a simple theorem of triangles.) the sides are integers because all the line lengths are. So we have a smaller all integer triangle. But there is no infinite sequence of ever smaller positive integers. Thus rt2 cannot be rational.
I think the term of art is “infinite descent”.
@dictum 3
Yes, a good point of usage.
Fits the coming election too.
@ken b
I may be missing something, but I think you need at least one more statement to your proof.
The smaller triangle might have rational, but not integer sides. There are sequences of infinitely decreasing rationals.
The ratio between the two triangles is (rt2 – 1) which is a rational ratio if rt2 is rational,and so the sequence of side lengths that your are saying doesn’t exist as integers does exist as rational if the original sides are rational.
You’ve shown that rt2 isn’t an integer, but that isn’t a proof that it’s not rational. Let me know what I’m missing about your proof.
DanR: This is actually covered in the other comments, but it might be easier to see with labels:
Our big triangle has four properties:
A1) It is a right triangle.
A2) It is isoceles, so P=T+S
A3) The legs are integers, so P (or T+S) is an integer
A4) The hypotenuse is an integer, so Q+R is an integer
We want to show that the smaller triangle has the same properties:
B1) It is a right triangle, because there is a right angle between Z (the tangent to the circle) and R (the extension of the diameter)
B2) It is isoceles, because it’s a right triangle (point B1) and the angle between R and S is known to be 45 degrees
B3) The leg R is an integer, because:
B3a) R=(Q+R)-Q
B3b) Q+R is an integer (point A4)
B3c) Q is an integer (point A3, plus the observation that Q=P because they are diameters of the same circle)
B4) The hypotenuse S is an integer because:
B4a) S=(T+S)-T
B4b) T+S is an integer (point A3)
B4c) T is an integer (because T=Z, being tangents to the same circle from the same point, Z=R (point B2) and R is an integer (point B3).
Dan R
What Steve said :)
T and Z are equal by a symmetry argument and we know Z is an integer because R is and Q is.
I gotta say to those finding it a bit tough that several of us here, Steve included, are trained mathematicians, and we ( or at least I) did not see it at a glance. Steve is being a bit droll in suggesting it’s an obvious proof. But it certainly is elegant.
T=Z was the missing (or unclear) point.
As an aside, readers can view this as related to the Good Puzzle Theorem. In cases like this the proof is only beautiful if every line or circle drawn is essential to the proof. Knowing this can be a help to piecing it together. This really is just right triangle for rt2 with a circle and one bit, Z, added. The proof really comes down to that line segment Z, which is the “added” bit. Ask yourself, what is so special about Z?
I remember a good “proof without words” from high school showing a unit square cut in half and one of the halves cut into quarters and one quarter cut into eighths etc to show that 1/2+1/4+1/8+…=1.
I’d like to translate this proof into the system of Euclid’s Elements. See this link: aleph0.clarku.edu/~djoyce/elements/elements.html First let me try justify the diagram itself:
1. That the circle exists is justified by Postulate 3
2. That the right angle is greater than the other angles of a right triangle is justified by by Proposition 1.32, Common Notion 3, and Common Notion 5.
3. That the hypotenuse is longer than the legs is justified by statement 2 and Proposition 1.19.
4. I don’t know how to justify that the circle intersects the interior of the hypotenuse, but it’s intuitively obvious given statement 3.
5. That the line containing the red segment exists is justified by Proposition 1.11
6. That the line containing the red segment and the line containing the lower leg are both tangent to the circle is justified by the corollary to Proposition 3.16
7. I don’t know how to justify that the line containing the red segment intersects the interior of the lower leg.
Now let me try to justify the statements in Steve’s comment #6:
B1 is justified by Definition 1.21.
B2. i. That the angle between R and S is half of a right angle is justified by Proposition 1.32, Common Notion 3, and Proposition 1.5
B2. ii. That the angle between R and Z is half of a right angle is justified by Proposition 1.32 and Common Notion 3.
B2. iii. That the smaller triangle is isosceles is justified by Proposition 1.6 and Definition 1.20.
B3. i. That Q=P is justified by Definition 1.15
B3. ii. That R is an integer is justified by statement A4, statement B3. i., and Proposition 5.6.
B4. i. I don’t know how to prove that T=Z, i.e. that tangents to the same circle to the same point are equal.
B4. ii. That T is an integer is justified by statement B2, statement B4. i., Common Notion 1, and statement B3.
B4. iii. That S is an integer is justified by statement A3, statement B4. ii, and Proposition 5.6
If anyone knows how to prove statement 4, statement 7, and statement B4. i., I’d appreciate it.
OK, it’s easy to prove statement B4. i. using this diagram: qph.ec.quoracdn.net/main-qimg-a2ec55bb267a0e726c48f8fdb14d509c?convert_to_webp=true
PO = PO, OA = OB by Definition 1.20, and PAO and PBO are right angles by Proposition 3.18. So by the side-side-right angle congruence theorem, which Euclid proves in the course of proving Proposition 3.14, PA = PB.
So now I just need to prove statements 4 and 7.
OK, statement 4 is justified by statement 3, Proposition 1.3, and Definition 1.15.
So now I just need to prove statement 7. Does anyone have any ideas?
Keshav
Not that I know Euclid but as for 4 the base of the triangle is a tangent and all points of the tangent line except the tangent point are outside the ciircle.
Keshav,
As for 7 you don’t need to prove it intersects “inside”. You only need to prove it intersects; if they intersect at all you have a triangle, and the similarity proves the rest. These are tangents not diametrically opposed (as the sides of the triangle are not colinear) so they do intersect.
But this it feels wrong smutzing up this gorgeous proof with numbered lemmas.
re 15 and Keshav’s 7
More simply you don’t need to prove S is smaller than anything, only that it’s integral. R < P suffices for the contradiction.
SL:
“Our big triangle has four properties:
A1) It is a right triangle.
A2) It is isoceles, so P=T+S
A3) The legs are integers, so P is an integer
A4) The hypotenuse is an integer, so Q+R is an integer”
?
The hypotenuse will never be an integer.
RichardD, don’t let Pythagoras hear you say that.
Richard D. (#17):
The hypotenuse will never be an integer.
That’s what we’re out to prove. Therefore we assume it and derive a contradiction.
The contradiction is this: If there are any such triangles, there is a smallest one. But if you draw the smallest one, then you can use it (as in the picture) to create an even smaller one. Nothing can be smaller than the smallest, which is a contradiction, proving the original triangle never existed in the first place.
Of course, proof by contradiction.
Did Euclid use this method of infinite sequence?
Richard D
The standard proof I learnt as a wee bairn is also an infinite decent and ascribed to Euclid. If rt2 = a/b then 2 = a*a/b*b so 2bb = aa but by primality of 2 a is even. so we write a = 2x. Then bb = 2xx so by primality b is even.
I’m not gettin’ this.
I get KenB’s argument—but with further elaboration: I understand KenB to argue that if the hypotenuse, rt2, were rational, then we’d be able to represent it by the ratio of two integers. So we propose two such numbers, a and b, in their lowest form–that is, having excluded all common (integer) factors. Then Ken proves that you can always find that a and b are even numbers, which contradicts the premise that these numbers were in lowest form. QED.
But I don’t get how that reasoning applies to a geometric diagram. The diagram does not (to me) express any idea about something being in lowest form. Indeed, how could it? What could it mean for a line segment to be “in lowest form”?
So let’s do another proof by contradiction: Let’s hypothesize that the triangle has an irrational hypotenuse. Now let’s apply the Landsburg axiom that if there are any such triangles there is a smallest one. Because we can always divide the length of each line segment by 2 and still produce a smaller version of the same triangle, this disproves the premise. Ergo the hypotenuse must be rational. QED.
In short, the statement “If there are any such triangles, there is a smallest one,” needs a little more unpacking.
Nobody, the logic of the diagram proof follows a similar structure. If rt2 is rational then you can draw that big triangle where all the sides are integers. If rt2 = a/b pick sides of size b^2 for example.
Now construct the smaller triangle. It,s sides are integers too. See the comments above.
Now we can repeat this process. Forever.
That gives us a sequence of ever smaller integers. But since the first integer side was finite and no side can be less than 0, we cannot have an infinite sequnce of them. So there’s the contradiction.
My comment about no infinite descending sequence of positive is logically the same as Steve’s assertion that there must be a least one (because both are about the properties of integers) but I think mine is more directly intuitive.
Pick an integer, say 341778093. How many integers are there that are both less than that, and greater than 0? Is it an infinite number?
Another aside. There’s a prejudice in modern mathematical education against visual proofs. Steve and I both deplore this tendency. This post is really a way to pique the interest of some readers in the pleasures and possibilities of such things. I have known the algebraic proof for 40 years but never saw this before. Part of the fun is figuring out the logic just from the visual hint.
Ok, that’s helpful.
And that’s very helpful. That explains the “If there are any such triangles, there is a smallest one,” statement, any why it doesn’t make sense to make the same assertion if we assume that rt2 is irrational.
Yet somehow it grates to use geometric proofs to distinguish between rational and irrational numbers. The elegance of geometric proofs is that we don’t worry about the absolute length of line segments. And, yeah, I guess the proof doesn’t worry about that. It just addresses their relative lengths. Still, I dunno; somehow it wrangles….
nobody.really (#26):
Yet somehow it grates to use geometric proofs to distinguish between rational and irrational numbers.
Ah, then you’ve thoroughly failed to see this as Pythagoras would.
Without the Pythagorean theorem, there is no reason to suspect that there are any irrational numbers. Indeed, the Pythagoreans more or less built a whole religion around the principle that all real numbers are rational. If you’d told them that the square root of two is irrational, they might well have said, “Well, okay, then there is no square root of two. That’s mildly interesting!”
But when they started playing around with triangles, they discovered that the hypotenuse of an isoceles right triangle (with legs of 1) has a length equal to the square root of two. Therefore the square root of two does exist, and now its irrationality undermines the whole religion. Hence the (perhaps apocryphal) death sentence for blabbing.
Key point: If you’re not doing geometry, you never have to worry about distinguishing rational numbers from irrational numbers in the first place. You just go on believing that all numbers are rational. It’s only the geometry that forces you to confront the phenomenon of irrationality, so to separate that phenomenon from geometry makes no sense.
This has been fun and educational (a form of proof I had either forgotten or wasn’t familiar with, contradiction-by-infinite-descent), and I’m using it to try to re-kindle my son’s interest in geometry (as opposed to “higher-level” math?). So thanks for that. Maybe kindling an interest in economics will be next…
I have only one thing to contribute to the thread: *Isosceles*
You saw celes? Where? I’ve been looking for mine.
This is an outstanding book, and large parts of it are accessible to a bright high school pupil (but not all: it is a university level textbook.)
https://www.amazon.com/Geometry-David-Brannan/dp/1107647835/ref=sr_1_1?ie=UTF8&qid=1478120260&sr=8-1&keywords=Geometry+cambridge+university+press
29-30
I saw Seles play Graf, great match.
Thanks for the link; he’s in HS but doing math at university…has always liked it but recently made a comment he’s finding calc a bit…I’ll use the word pedantic? Not sure if that means he prefers more conceptual or applied. Maybe some of you can relate? Thought of it b/c this post gave me a new angle on geometry (ahem).
Yo Iceman!
I bought my son this when he finished high school and told him he’d thank me later. He was skeptical. He thanked me later.
https://www.amazon.com/Calculus-Intuitive-Physical-Approach-Mathematics/dp/0486404536/ref=sr_1_2?ie=UTF8&qid=1478201296&sr=8-2&keywords=dover+calculus
I cannot resist. It’s a subtlety glossed over by all the comments here (but I mention it in 2). Despite all the comments about “integer length” there is no such thing!
What there are are integral numbers of multiples of any given set length. And the question Steve refers to in 27 is really, are all lengths commensurate? And that means if I line up a bunch of the first ( so an integral number) with a bunch of the second, will the lengths ever match? This proof shows that they are not all commensurate by displaying a pair that aren’t. That’s not obviously a question about numbers as fractions of integers, and it was quite an achievement of the ancient Greeks to formulate that geometric question in that way, and answer it algebraically as Euclid did. But this proof is in an important sense simpler. We don’t need results of prime number theory, or to embrace the reduction of this question to one about fractions. We can see more directly that all sides are integer multiples of the set length, and the proof adumbrated above carries through. Replace “integer” with “integral number of lengths.”
32 – thank u much appreciated – preface sounds intriguing, could be just what the dr ordered. Might enjoy it myself (at least as much of the 800 pages as I can digest)
@Ken B If you notice, my proof is actually about integer multiples of fixed lengths and not simply thinking of lengths as integers. That’s why I repeatedly used Euclid’s Proposition 5.6: “If two magnitudes are equimultiples of two magnitudes, and any magnitudes subtracted from them are equimultiples of the same, then the remainders either equal the same or are equimultiples of them.” What that means p in modern terminology is that if m and n are two integers greater than 1 and x is a magnitude, and mx > nx, then either mx – nx = x or mx – nx = kx for some integer k greater than 1. (The thing is that Euclid didn’t think of 1 as a number.)
@Keshav
Maybe so but not explicitly. There is no explicit mention in 11. Look at 11b 3.2 for instance. I have no doubt all the mathematicians understand the point I made in 33, you included. Not all readers are mathematicians though.