Greg Mankiw has a provocative post on how wages are affected by a cut in the tax rate on capital income. The short version: The effect is huge. If the government commits to a permanent tax cut that costs it $1 in revenue this year, then in the long run, annual wage payments will rise by $1.50 (and the annual revenue shortfall will be even less than $1).
.
That strikes me as huge. Wages grow by more than government revenue falls — in fact, by a factor of about 1/(1-t), where t is the initial tax rate. Mankiw’s $1.50 comes from plugging in an initial tax rate of 1/3.
Although Mankiw’s calculation is simple, straightforward and convincing, it managed to drive me crazy for a substantial chunk of a day, because I didn’t really understand what was driving it. Now I do. So let me explain.
First, the quick explanation for the wonks. Start with this graph of the demand for capital:
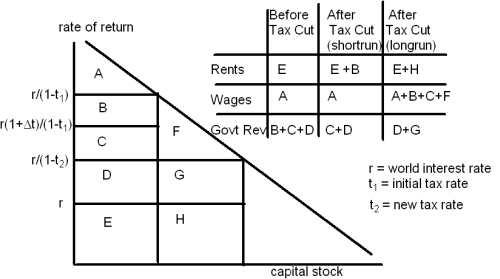
When the government cuts the tax rate on capital income from t1 to t2, short-run government revenue falls by B and long-run wage payments rise by B+C+F. For a small tax cut, F is negligible, so the ratio we’re looking for is (B+C)/B, which is easily calculated to be 1/(1-t2). If t2 is about 1/3, this ratio is about 3/2. So a $1 cut in shortrun annual government revenue yields a $1.50 increase in longrun annual wage payments.
Notice that only one point on the capital demand curve ever comes into play here (namely the upper right-hand corner of area B). The rest of the curve is entirely irrelevant, which answers Mankiw’s question (see his blog post) about why his result is independent of the production function.
For those who want a bit more detail:
The government’s revenue is a product of three factors:
- The tax rate.
- The pre-tax income earned by each unit of capital.
- The total stock of capital.
These are the effects captured in the graph by areas B, C and G. In the short run, only the first of these matters.
In the long run, total wages go up for two reasons:
- Areas B and C, which are no longer being claimed by the government, are initially pocketed by capitalists. But competition does not allow those capitalists to continue earning excess returns, so they can’t continue to pocket these areas. Since the government isn’t taking them, and the capitalists can’t hold on to them, that leaves the workers as the residual claimaints.
- Because of new investment, more workers are hired. The effect of this shows up in Area F.
I spent a half a day being confused because I thought that the last of these effects was important, and I didn’t see how its size could fail to depend on information we haven’t got about the production function. Once I realized that F has nothing to do with it, the intuition became clear. Mankiw’s result is driven completely by the the fact that the ratio (B+C)/C is exactly 1/(1-t2) where t2 is the post-tax-cut-rate.
In other words, Mankiw’s result, as I read it, is only incidentally about wages. It’s fundamentally about the ratio of the long-run to the short-run government revenue shortfall (not counting the correction to the long-run shortfall that is due to new investment). That’s relevant to wages only because the long-run shortfall happens to end up entirely in the hands of workers. I trust this observation will not impair the workers’ appreciation for their windfall.
One more thing: Now that I understand this, I don’t see any particular reason the long-run government revenue shortfall should be smaller than in the short-run, as Mankiw says is “typically the case”. The short-run shortfall is B; the long-run shortfall is B+C-G. This claim of Mankiw’s seems to require G>C, and I don’t see any particular reason to expect that. (Perhaps this was intended as an empirical claim?)



In your grid in the upper-right corner, I don’t understand why in the short run after the tax cut, amount B moved from “govt rev” to “rents”. For sure it moves out of the “govt rev” row, but why does it move to “rents”? I assumed “rents” is the interest you’re paying on the capital you borrowed. But if the amount of borrowed capital stays the same in the short run, why does “rents” change? Or was that a typo and it’s supposed to move into the “wages” row.
Bennett: In the short run B is a transfer from the govt to the capitalists. Anything collected by the capitalists I call a rent.
Are we sneaking in the assumption that r doesn’t increase with increasing capital stock?
Darin Johnson: We’re not sneaking in this assumption; Mankiw is making it explicitly.
Is this somehow related to the claim that taxation causes a large deadweight loss?
Daniel R. Grayson:
No, quite the opposite.
A tax cut has two effects: It redistributes existing income and it reduces deadweight loss. In the present context, the size of the redistribution is of first order in the tax cut and the size of the reduction in deadweight loss is of second order — so to first order, the deadweight loss issues are quite irrelevant.
The reason it took me a little while to understand Mankiw’s post was that a) it’s clear that the form of the production function affects the size of the deadweight loss reduction, b) I thought the deadweight loss reduction was key here, and yet c) Mankiw’s result is independent of the form of the production function. This seemed paradoxical. My mistake was in b). This result has absolutely nothing to do with deadweight loss.
I’m not seeing why when the government cuts the tax rate on capital income from t1 to t2, short-run government revenue falls by B rather than B + C.
If the tax rate falls and in the short term the amount of capital demanded stays the same then why won’t revenue immediately fall from the point marked r/(1-t1) to the point marked r(1-t2) ?
(I see that in the long run amount of capital demanded increases and govt revenue increases again by G)
Rob Rawlings: The pre-tax rate of return on capital is initially r/(1-t1), and the tax on that return is t1, so the tax on capital is t1 x r/(1-t1). After the tax cut, the pre-tax rate of return is unchanged (because the capital stock is unchanged) but the tax on that return is t2, so now the tax on capital is t2 x r/(1-t1). The difference between those two taxes on capital is the height of rectangle B.
Why would a comparison between the long-run gain in wages and the short-run loss in revenue even be relevant?
Neil: I believe the motivation is this: 1) A comparison between the long-run gain in wages and the long-run loss in revenue is intrinsically interesting, but difficult to calculate. 2) In many circumstances, it’s reasonable to think that the short-run loss in revenue is an upper bound on the long-run loss in revenue. 3) Therefore a comparison between the long-run gain in wages and the short-run gain in revenue at least gives you a bound on the ratio you really want to compute, and fortunately you can compute it — so you do.
What are the assumption being made regarding the actual number of people employed?
So as usual I think I kind of understand the math, but I don’t understand why reality doesn’t align with the math. In particular you say:
Areas B and C, which are no longer being claimed by the government, are initially pocketed by capitalists. But competition does not allow those capitalists to continue earning excess returns, so they can’t continue to pocket these areas. Since the government isn’t taking them, and the capitalists can’t hold on to them, that leaves the workers as the residual claimaints.
Because of new investment, more workers are hired. The effect of this shows up in Area F.
And then I read studies of actual effects of actual tax cuts in the actual world, and they don’t agree with this, at all. For example: http://www.businessinsider.com/study-tax-cuts-dont-lead-to-growth-2012-9 (I think the headline is sensationalist garbage but ignore that.)
That’s from 2012. Then there’s this from 2010: https://www.cbpp.org/research/cutting-state-corporate-income-taxes-is-unlikely-to-create-many-jobs
It’s a lot of words, and much of it is an argument based on states’ needs to maintain a balanced budget each year, necessitating immediate cuts to offset immediately lost revenue. But it also appears to be an argument based in some experience to say that cutting rates does not in fact cause more money to end up in the pockets of workers.
Are these data wrong? Out of date? Is there any publication of real-world data showing that the mathematically predicted effect actually comes to pass?
This piece – https://www.nytimes.com/2017/04/05/business/dealbook/tax-cuts-job-growth-trump.html – from just recently is notably long on words and short on data. It argues that other factors overwhelm the theoretical results, leading to non-obvious and even reverse results such as the economic boom that followed tax increases in 1993.
Awesome! Minor typo- shouldn’t r(1+ (Delta t))/(1-t1) be R(1 x (Delta t))/(1-t1)
Ugh, r not R.
Alex Tabarrok:
No, I think it’s correct as shown:
1) Prior to the tax cut, capital must rent for an after-tax rate of r and hence a pre-tax rate of r/(1-t1).
2) Prior to the tax cut, the government taxes that rent at the rate t1 and so collects t1 r/(1-t1) per unit of capital.
3) Immediately after the tax cut, capital continues to rent for a pre-tax rate of r/(1-t1).
4) Immediately after the tax cut, the government taxes that rent at a rate t2 and so
collects t2 r/(1-t1) per unit of capital.
5) Therefore, from 2) and 4), the tax cut causes a short-run government revenue shortfall of S=(t1-t2) r/(1-t1) per unit of capital.
6) The height of rectangle B is [r-r(1+t2-t1)]/(1-t1) , which is the same quantity we called S in point 5).
7) Therefore the height of rectangle B is the short run govt revenue shortfall per unit of capital, so rectangle B is the total short run govt revenue shortfall.
The above comes out right, using the expression r(1+t2-t1)/(1-t1) just as it’s shown. So I believe there is no typo.
Alan Wexelblat:
I just briefly followed your first link, and it’s quite irrelevant here. Tax cuts can, in principle, lead to redistribution and/or growth. Mankiw’s calculation is *entirely* about the redistributive effect of a capital tax cut and ignores the growth effect entirely. (This is exactly the point I missed on a first reading, and it’s why I initially had trouble following his argument.) The article you linked to is entirely about the growth effect. That’s completely separate from anything Mankiw is computing.
In terms of the graph, the tax cut causes workers to gain B+C through redistribution and F through economic growth. Mankiw is computing B+C. The first of your links (and probably the others, which I haven’t looked at yet) is talking about F.
Got it! I was calculating S, the height of the rectangle B. Thanks!
Can I safely assume that other types of taxes do not have the same effect on wages? If tax collection neutrality is required, I assume that a different type of tax increase needed to make this tax collection neutral would lower wages by less than the capital income tax would increase it?
Pat: Good point. There is an implicit assumption here that the tax revenue is not being used for anything. If it is being used for something, then either that revenue will have to be replaced via some other tax, or valuable government services have to disappear. In the latter case, people might want to work more (if the govt is no longer providing you with Wheaties, you’ll want to buy more Wheaties for yourself, in which case you’ll work more hours to earn your Wheaties), which could cause total wage payments to go up, though not in a way that workers are happy about. In the former case, the effect on wages depends on all sorts of things including, of course, which tax is raised.
Steve (#19),
Is there something about a tax on capital income that has an unusually large effect on wages that other taxes don’t? (Is there a tax that you’d recommend instead if we’re forced to be revenue neutral?) I’m one of those people that loves economics but struggles with pictures. (I’m having flashbacks to Ron Schmidt’s class and I wasn’t good then either!)
Here are where my numbers come out:
Assumptions
– Nominal GDP: $19 trillion
– Effective corporate tax rate: 18.6% (equal to 35% nominal)
– Proposed new tax rate, nominal, 25%
– Corporate taxes as share of GDP: 1.6%; in dollars, cc $300 bn
Thus,
1/(1-t) = 1.23, not 1.5, because effective, not nominal, rates would seem to matter in terms of economic effect
A reduction in the tax rate to 25% results in an assumed effective tax rate of 13.3%, and a reduction in total corporate taxes paid to cc $215 bn.
Thus, tax savings equal $85 bn on initial taxes paid of $300 bn, which increases profits by 5.3% immediately, with valuations presumed to follow pari passu (ie, DOW to 24,600).
Labor constitutes 70% of the economy, which translates into $13.3 trillion. The wage effect is 1.23 x the savings of $85 bn, or $105 bn. This increases workers wages, to the extent such savings affect workers as a class (as opposed to the workers in question at those companies) by increasing wages 0.8% over the long run.
Thus, corporations see an immediate increase in profits of 5.3% and workers see an eventual gain of 0.8%.
As a practical matter, it looks to me like Summers is right. For corporations, there is an immediate benefit to the bottom line. For workers, there is some gain over time which will essentially be washed out as noise.
Or do I have this wrong?
I’m not an economist, and I only barely understand the math, but I know for a fact that “obvious” conclusions from mathematical analysis, esp. in economics, can be quite off the mark in real life. Specifically, this paragraph set off my alarm bells:
“Areas B and C, which are no longer being claimed by the government, are initially pocketed by capitalists. But competition does not allow those capitalists to continue earning excess returns, so they can’t continue to pocket these areas. Since the government isn’t taking them, and the capitalists can’t hold on to them, that leaves the workers as the residual claimaints.”
Alan above also called this one out. I think you have too much faith in competition.
Ben U: So is it your guess that the capitalists are uninterested in profit, or that they’re too stupid to pick up on the evident profit opportunities?
I think what Ben U was trying to say is that in our non-perfectly competitive real world, returns to capital include a chunk of what you draw as A as well as rectangle E. So, yes, the capitalists will indeed be smart enough to pick up “evident profit opportunities”, but this activity won’t restrict the profit share to E, since this activity isn’t already restricting the profit share to E.
But that’s a quibble. I don’t have a problem with the perfect-competition-as-illustration approach – and you have made explicit the time dimension in what other commentators have tended to treat as an instantaneous change. Thanks a bunch for that.
In my perfect world, the ‘corporate’ tax rate would be zero – with a progressive income tax providing the platform to debate (and manage) all the distributional issues. Alas, Mankiw’s “exercise” doesn’t get us much closer to that kind of discussion.
Seems to me that Mankiw is trying to put lipstick on a pig. Let’s state it this way: We are cutting taxes on capital now which gives an equal and immediate windfall to capitalists now, which may be replaced by gains to labor in the future, which may be greater due to reduced DWL. Now let’s ask some questions any sensible person would.
Q: How far in the future?
A: Can’t say, until enough capital flows in. Could be decades.
Q: Aren’t future gains worth less than immediate?
A: Duh, yeah.
Q: How are the lost tax revenues to be made up?
A: We’ll tell you a Laffer curve fairy tale or that we’ll cut government waste, but the truth is we will increase taxes on labor since we are cutting taxes on capital.
Q: And I am supposed to buy this?
A: You will, my friend, you will.
Tom Barson: +
Any economists out there know of an economic rationale for a non-zero corporate tax? Certainly would be easier to sort out the overall progressivity & distributional effects on a single “platform”. Maybe that obfuscation IS the rationale
The result that the “static” Furman ratio is 1/(1-t2) seems to hinge crucially on the assumption that in the initial period which we consider “static,” the pre-tax return on capital remains at r/(1-t1), even after the tax rate has been cut to t2. But if there is some intermediate period — still before the capital stock adjusts, but after the pre-tax return to capital has fallen to r/(1-t2), then over this period the gov’t revenue loss will be larger. In fact, it will be exactly equal to the long-run wage gain (net of any growth effects), rather than 1/(1-t2) smaller. In other words, taking into account the effect of a lower pre-tax return on capital (but not yet a larger capital stock), the redistribution effect from government revenue to wages in this model is one for one, not more than one for one (which at some level makes sense — how can redistribution be more than one-for-one? only if we are assuming that the fall in the pre-tax return on capital has no impact on gov’t revenue until the capital stock adjusts). I guess it boils down to how exactly we define the period of time we are calling “static.”